Здравствуйте, Sonya2006f!
Чтобы восстановить неполный квадрат суммы, нужно представить крайние члены данной формулы в виде числа со степенью.
Разложение чисел на простые множители:
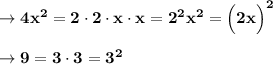
Теперь когда мы знаем, как представить данные члены в виде числа со степенью, запишем формулу, по которой выполнялось разложение.
Формула сокращённого умножения:
НЕПОЛНЫЙ КВАДРАТ СУММЫ: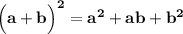 
.
Зная, что первоначально выражение имело вид 
, перемножим по формуле эти члены между собой и получим ответ на Ваш вопрос.
Разложение данного выражения на множители:
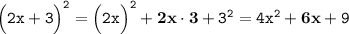
Окончательный ответ данной задачи:
Неполный квадрат суммы данного выражения - "6x".
С Уважением, NeNs07.
Здравствуйте, Sonya2006f!
Чтобы восстановить неполный квадрат суммы, нужно представить крайние члены данной формулы в виде числа со степенью.
Разложение чисел на простые множители:
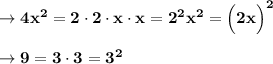
Теперь когда мы знаем, как представить данные члены в виде числа со степенью, запишем формулу, по которой выполнялось разложение.
Формула сокращённого умножения:
НЕПОЛНЫЙ КВАДРАТ СУММЫ: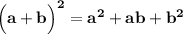 
.
Зная, что первоначально выражение имело вид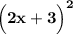 
, перемножим по формуле эти члены между собой и получим ответ на Ваш вопрос.
Разложение данного выражения на множители:
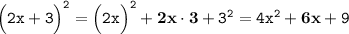
Окончательный ответ данной задачи:
Неполный квадрат суммы данного выражения - "6x".
С Уважением, NeNs07.
1)х(5-2у)
2)-4а(4)(1-5а(6))
3)(3х-4у)(a+b)
4)(м-2n)+4y(2n-m)
5)(a-b)(4+c)
6)(mn-1)(mn+1)(m+n)
1)x(2)-36
2)16b(2)-1
3)x(14)-q(10)
4)0.09p(6)-0.04q(8)
5)n(10)-m(12)
1)-a(2)-8a-9
2)8y-31
Объяснение:
3(10)-чисто в дужках це степінь