Нет точки максимума
Объяснение:
Рассмотрим функцию
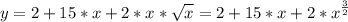
Так как в составе функции участвует квадратный корень, то область определений функции: x≥0, то есть D(y)=[0; +∞).
Чтобы найти экстремумы (локальные минимумы и максимумы) будем исследовать функцию с производной функции. Вычислим производную функции:
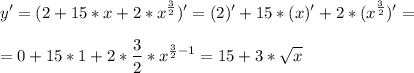
Так как 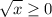 , то
, то
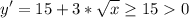
для любого x∈D(y). Это означает, что данная функция монотонно возрастает в D(y). Отсюда следует, что у функции нет точки максимума.
Так как функция монотонно возрастает в D(y), то минимальное значение в D(y)=[0; +∞) принимает при x=0: y(0)=2.
1)) Вы, действительно, потеряли один корень...
там получится квадратное уравнение: (cosx)^2 = 0.5
решение: cosx = + - V2/2
для cosx = +V2/2 Вы записали тоже не полностью: x = pi/4 + pi k и x = = -pi/4 + pi k
а для cosx = -V2/2 еще добавятся: x = 3pi/4 + pi k и x = = -3pi/4 + pi k
и ответ в учебнике ---это объединение всех четырех решений!!
если посмотреть расположение этих ответов на единичном круге, то можно заметить, что pi/4 "отстоит" от 3pi/4 ровно на pi/2... и 3pi/4 "отстоит" от -3pi/4 ровно на pi/2...
т.е. это объединенное решение: x = pi/4 + (pi/2) * k
а Вы просто потеряли корни...