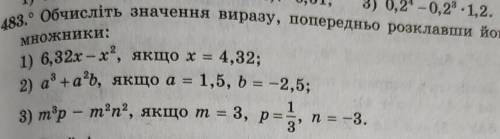
Объяснение:
Проблемы, указанные автором: проблемы демографии, безработица, неполное использование социальных и экономических возможностей общества, дефицит и нерациональное управление ресурсами, неэффективность принимаемых мер, инфляция, отсутствие безопасности и гонка вооружений, загрязнение среды и разрушение биосферы, заметное уже сегодня воздействие человека на климат.
Фрагмент текста: «нынешняя, полная чудес и противоречий фаза прогресса, принеся человеку множество щедрых подарков, в то же время глубоко изменила нашу маленькую человеческую вселенную, поставила перед человеком невиданные доселе задачи и грозит ему неслыханными бедами».
Примеры противоречивости прогресса:
1) развитие атомной электроэнергетики позволяет повысить эффективность производства, однако может быть опасным для окружающей среды и человека в случае аварий на АЭС;
2) использование Интернета позволяет увеличить темы коммуникации между людьми, при этом может вызвать определённую зависимость и другие психологические проблемы;
3) развитие биоинженерии и исследований в области генетики выводит на новый уровень возможности медицины по лечению и профилактике болезней, но при этом создаёт множество этических проблем (например, клонирование).
Мир стремительно меняется, особенно в области новых технологий, человек не успевает адаптироваться к новым возможностям, и это порождает ряд проблем (технологические аварии, структурная безработица и т. д.).
В условиях крайней нестабильности и неустойчивости человеку психологически трудно справляться с вызовами времени, и это, в свою очередь, усиливает трудность адаптации к новым изменениям.
Изменения культуры и общества происходят неравномерно: для разных регионов мира актуальны разные запросы, что делает затруднительным поиск ответов в вопросе решения глобальных проблем.
Откуда задание и тот ли это предмет?
Дана функцию f(x) = (x² - 3x) / (x - 4 ).
1 ) Найдите наибольшее и наименьшее значения функции на данном промежутке [-1; 3].
2 ) Найдите промежутки возрастания и убывания и точки экстремума функции .
ответ: 1 ) наибольшее 1 ; наименьшее - 0,8 .
2 )
Функция возрастает: x ∈( -∞ ; 2 ] и x ∈[ 6 ;∞) .
Функция убывает x∈[2 ; 4) и x ∈(4 ;6] ;
Точки экстремумов: x =2 точка максимума и x = 6 точка минимума .
Объяснение: D(f) : ( - ∞ ; 4) ∪ (4 ; ∞ ) [ R \ {4 } ]
( u(x) /v(x) ) ' = ( u'(x)*v(x) - u(x)*v'(x) ) / v²(x)
f ' (x) = ( (x² - 3x) / (x - 4 ) ) ' =( (x² - 3x) ' *(x - 4 ) - (x² - 3x)*(x-4) ' ) / (x-4)² =
( (2x - 3)*(x - 4 ) - (x² - 3x)* 1 ) / (x-4)² = (x² - 8x +12) / (x-4)² =(x-2)(x-6) / (x-4)².
f ' (x) = 0 ⇔(x-2)(x-6) / (x-4)² =0 ⇒ x₁ =2 , x₂ = 6 .
f'(x) не существует в точке x =4 , но в этой точке не существует и функция
1)
* * * x₂ = 6 ∉ [ -1 ; 3 ] * * *
x₁=2 ∈ [ -1 ; 3 ] f (x₁ ) =f (2 ) =(2² -3*2) /(2 - 4) = 1 ;
f (a ) =f (-1 ) =( (-1)² -3*(-1) ) /( (-1) - 4) = - 4/5 = - 0,8 ;
f(b) = f(3) = (3² - 3*3) /(3 -4) = 0
На промежутке [-1;3] наибольшее значение функции равно 1 (если x=2 ), наименьшее значение -0,8 (если x= - 1 ) .
2)
Промежутки возрастания и убывания и точки экстремума функции .
f ' (x) = 0 ⇔(x-2)(x-6) / (x-4)² =0 ⇒ x₁ =2 , x₂ = 6 .
Функция возрастает , если f ' (x) ≥ 0
Функция убывает , если f ' (x) ≤ 0
По методу интервалов
f '(x ) + + + + + + + + + + [ 2 ] - - - - - - - - - - [ 6] + + + + + + +
f (x ) ↑ (возрастает) ↓ (убввает) ↑ (возрастает)
Функция возрастает: x ∈( -∞ ; 2 ] и x ∈[ 6 ;∞) .
Функция убывает x∈[2 ; 4) и x ∈(4 ;6] .
x =2 и x=6 точки экстремумов ( производная функции меняет знак при прохождения через эти точки )
x =2 точка максимума , f(2) = 1
x =6 точка минимума , f(6)=(6² -3*6) /(6 - 4) =(36-18)/ 2=9.
1) 8,64
2) -2,25
3) -72
Объяснение:
1) 6,32x - x² при x = 4,32
6,32x - x² = x(6,32 - x) = 4,32(6,32 - 4,32) = 4,32 * 2 = 8,64
2) a³ + a²b при a = 1,5; b = - 2,5
a³ + a²b = a²(a + b) = 1,5²(1,5 - 2,5) = 2,25 * (-1) = -2,25
3) m³p - m²n² при m = 3; p = 1/3; n = - 3
m³p - m²n² = m²(mp - n²) = 3²(3 * 1/3 - (-3)²) = 9(1 - 9) = 9 * (-8) = -72