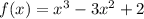
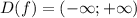- множество всех действительных чисел.
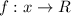называется четной, если выполняется равенство: 
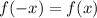, а нечетной -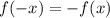 
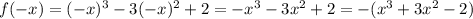
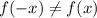и 
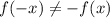, значит функци ни чётная ни нечётная.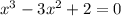
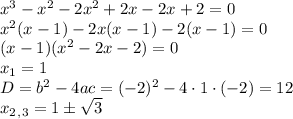
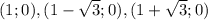- точки пересечения с осью Ох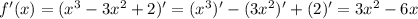
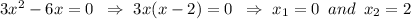
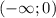и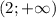 
, а убывает на промежутке - 
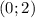. В точке 
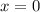функция имеет локальный максимум, а в точке 
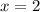- локальный минимум. 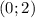- относительный максимум. 
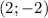- относительный минимум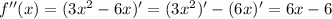
1) 1= -1*4+3
2)-5= -1*3+ (-2)
K и б можно подставлять