Объяснение:
((a+7)\(a-7)-(a-7)\(a+7))\(14\(a^2-7a))
Приведем дроби в скобке к общему знаменателю a^2-49, домножив первую дробь на (a+7), а вторую на (a-7):
((a+7)^2-(a-7)^2)\(a^2-49)
По формуле разности квадратов:
((a+7-a+7)(a+7+a-7))\(a^2-49)
14*2a\a^2-49
28a\a^2-49
Представим деление одной дроби на другую умножением первой на перевернутую вторую:
(28a*(a^2-7a))\(14*(a^-49))
Вынесем в числителе "а" за скобку, а в знаменателе разложим скобку на множители:
(28a^2*(a-7))\(14(a-7)(a+7))
Сократим дробь:
2a^2\(x+7)
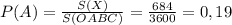
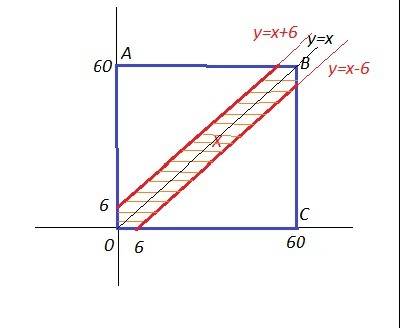
переносишь все из правой части в левую
получается в знаменателях (х-1) (х+1) и ( х^2 - 1)
х^2-1 = (х-1)(х+1)
умножаешь все на общий множитель, как раз (х-1)(х+1)
получается к 1ой дроби доп множитель (х+1), ко второй (х-1) и к третей 1 соответственно
раскрываеш скобки ...
2х^2 +2х + 3х-3-3х-1=0
сделав вычисления получаем
2х^2 +2х-4=0
можешь разделить все на 2 ( х^2 +х-4)
получается в любом случае
по теореме виетта
х1 + х2 = -1
а х1*х2 = -2
ответ х1= -2
х2 = 1