Объяснение:мы умеем сравнивать дроби с одинаковыми знаменателями и одинаковыми числителями, числители у нас разные, но приводить к общему знаменателю мы умеем.
сравним
2/9 и 5/12, общий знаменатель 36,
2*4/(9*4) и 5*3/(12*3)
8 <15 значит 2/9 < 5/12
сравним
5/12 и 4/15, общий знаменатель 60
5*5/(12*5) и 4*4/(15*4)
25>16
значит 5/12 > 4/15
теперь мы знаем что 5/12 самое большое. надо сравить
2/9 и 4/15 общий знаменатель 45
2*5/(9*5) и 4*3/(15*3)
10 <12
значит 2/9 < 4/15
итого самая маленькая это 2/9 потом 4/15 и 5/12
Другой вариант решения привести все три дроби к одному общему знаменателю.
9=3^2 12=3*2*2 15=3*5, НОК= 2*2*3*3*5=180
2/9=2*20/(9*20)=40/180
5/12=5*15/(12*15)=75/180
4/15=4*12/(15*12)=48/180
в таком виде сравнить дроби просто.
2/9<4/15<5/12
3/8, 5/18 и 10/21
можно применить второй , но тут цифры будут неприятные, так что давайте всё-таки попарно
3/8 5/18
3*9/(8*9) 5*4/(18*4)
27/72 > 20/72
3/8 и 10/21
3*21/(8*21) 10*8/(21*8)
63/168 < 80/168
мы получили что 3/8 меньше 10/21 и больше 5/18, значит последнюю пару сравнивать не нужно можно сразу писать ответ
самое большое это 10/21 потом 3/8 и 5/18
Первое задание
Число делится на 4, если число, составленное из последних двух цифр, делится на 4. В данном случае это 37628 (ведь 28 делится на 4).
ответ: 37628.
Второе задание
Преобразуем это число по правилам действий со степенями:
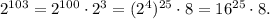
Число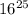 
оканчивается на 6, потому что любое число, оканчивающееся на 6, в любой степени тоже оканчивается на 6. Затем, если мы умножим это число на 8, то получим число, оканчивающееся на 8 (потому что 
).
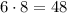ответ: на 8.
Третье задание
Преобразуем выражение по правилам действий со степенями:
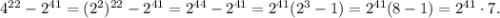
ответ: на 7.
***
Если будут какие-нибудь вопросы — задавайте.
Если мой ответ оказался полезен, отмечайте его как «лучший ответ».
Объяснение:
Можно лучший ответ