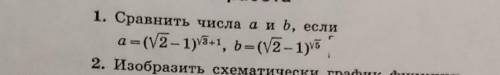
Объяснение:
|x -1| + |x +3| ≤ 4
Решим это неравенство методом интервалов.
Найдем нули подмодульных выражений:
х - 1 =0 → х = 1
х + 3 = 0 → х = - 3
Эти значения разбивают числовую ось на три интервала:
х ∈ (-∞; - 3] ; (-3; 1]; (1; + ∞)
Решим заданное неравенство на каждом из этих промежутков.
1) 1) x∈ (-∞; - 3], при этом неравенство примет вид:
- (х - 1) - (х + 3) ≤ 4
-х + 1 - х - 3 ≤ 4
-2х ≤ 6
х ≥ - 3
Пересекая найденное решение x∈ [- 3; +∞) c рассматриваемым интервалом x∈ (-∞; - 3] , получаем решение x = - 3
2) х ∈ (-3; 1]
- (х - 1) + х + 3 ≤ 4
0*х ≤ 4 → х - любое число. Учитывая интервал, х х ∈ (-3; 1]
3) х ∈ (1; + ∞)
х - 1 + х + 3 ≤ 4
2х ≤ 2
х ≤ 1 → х ∈ (- ∞; 1]
Для получения окончательного ответа объединим полученные решения:
x ∈ [- 3] ∪ (-3; 1] ∪ (- ∞; 1]
ответ: х ∈ [-3; 1]
Сторона данного треугольника а(3) равна Р:3=6√3:3=2√3 дм
Формула радиуса окружности, описанной около правильного треугольника:
R=a/√3 =>
R=2√3:√3=2 дм
Формула стороны правильного многоугольника через радиус вписанной окружности:
а(n)=2r•tg(180°:n), где r – радиус вписанной окружности, n – число сторон,
Для правильного шестиугольника tg(180°:n)=tg30°=1/√3
a₆=2•2•1/√3=4/√3
P=6•4/√3=8√3 дм
—————
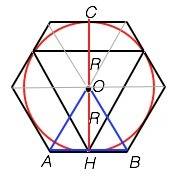
Как вариант: Правильный шестиугольник состоит из 6 равных правильных треугольников.
На рисунке приложения ОН - радиус описанной около правильного треугольника окружности и в то же время высота одного из 6 правильных треугольников, все углы которого 60°; АВ - сторона шестиугольника. Задача решается с т.Пифагора.
Объяснение:
...........................................