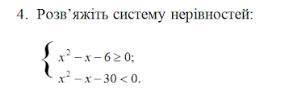
Сократите дробь:а)(36-а)/(6-√а)=((6-√а)(6+√а))/(6-√а)=(6+√а)
б)(5-√5)/(√15-√3)=(√5(√5-1))/(√3(√5-1))= √(5/3)
освободитесь от знака корня в знаменателе: а)15/√5
15=√5*√5*3,соответственно 15/√5=(√5*√5*3)/√5=3√5
б)5/(√13 - √3) здесь используется метод домножения на сопряженное, соответственно:
5/(√13 - √3) =5(√13 + √3) /(13-3)=(√13 + √3)/2
докажите что значение выражения 4/2√3 - 1 - 4/2√3 - 1 является рациональным числом:
4/2√3 - 1 - 4/2√3 - 1 это выражение равно -2, так как если мы переставим слагаемые по-другому,получим:
4/2√3 - 4/2√3 -1 -1, отсюда видно что:
4/2√3 - 1 - 4/2√3 - 1= -2
упростите выражение а)√х в шестой степени = х^3 так как √х^6= x^(6/2) и соответственно это x^3
Сократите дробь:а)(36-а)/(6-√а)=((6-√а)(6+√а))/(6-√а)=(6+√а)
б)(5-√5)/(√15-√3)=(√5(√5-1))/(√3(√5-1))= √(5/3)
освободитесь от знака корня в знаменателе: а)15/√5
15=√5*√5*3,соответственно 15/√5=(√5*√5*3)/√5=3√5
б)5/(√13 - √3) здесь используется метод домножения на сопряженное, соответственно:
5/(√13 - √3) =5(√13 + √3) /(13-3)=(√13 + √3)/2
докажите что значение выражения 4/2√3 - 1 - 4/2√3 - 1 является рациональным числом:
4/2√3 - 1 - 4/2√3 - 1 это выражение равно -2, так как если мы переставим слагаемые по-другому,получим:
4/2√3 - 4/2√3 -1 -1, отсюда видно что:
4/2√3 - 1 - 4/2√3 - 1= -2
упростите выражение а)√х в шестой степени = х^3 так как √х^6= x^(6/2) и соответственно это x^3
1) x² - x - 6 ≥ 0
(x - 3)(x + 2) ≥ 0
+ - +
______[- 2]______[3]_______
////////////// ////////////////
x ∈ (- ∞ ; - 2] ∪ [3 , + ∞)
2) x² - x - 30 < 0
(x - 6)(x + 5) < 0
+ - +
_______(- 5)______(6)______
///////////////////
x ∈ (- 5 ; 6)
Окончательно :
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ /////////////////////////
______(- 5)_____[- 2]_______[3]_____(6)_____
////////////////////////////////////////////////
ответ : x ∈ (- 5 ; - 2] ∪ [3 ; 6)