Первое выполнение функции
a (x) = 2, b (y) = -4
p (a1) = (x + y) / 2 = (2 + (-4)) / 2 = -2 / 2 = -1
q (b1) = (x - y) / 2 = (2 - (-4)) / 2 = 6 / 2 = 3
Вывод
a = 2, b = -4, a1 = -1, b1 = 3
Второе выполнение функции
(изменили возвращаемые переменные)
a (x) = 2, b (y) = -4
p (b1) = (x + y) / 2 = (2 + (-4)) / 2 = -2 / 2 = -1
q (a1) = (x - y) / 2 = (2 - (-4)) / 2 = 6 / 2 = 3
Вывод
a = 2, b = -4, a1 = 3, b1 = -1
Третье выполнение функции
(изменили входные данные)
a (x) = -4, b (y) = 2
p (a1) = (x + y) / 2 = (-4 + 2) / 2 = -2 / 2 = -1
q (b1) = (x - y) / 2 = (-4 - 2) / 2 = -6 / 2 = -3
Вывод
a = 2, b = -4, a1 = -1, b1 = -3
Радиус проведённый в точку касания перпендикулярен касательной.
В четырёхугольнике сумма углов равна 360°.
В четырёхугольнике EOFC:
∠ECF = 360°-∠EOF-∠CEO-∠CFO = 360°-102°-90°-90° = 78°.
В треугольнике сумма углов равна 180°.
В ΔABC:
∠BAC = 180°-∠ABC-∠BCA = 180°-90°-78° = 12°
В четырёхугольнике BEOD:
∠EOD = 360°-∠ODB-∠DBE-∠BEO = 360°-90°-90°-90° = 90°
В четырёхугольнике DOFA:
∠DOF = 360°-∠OFA-∠FAD-∠ADO = 360°-90°-12°-90° = 168°
ответ: ∠A=12°, ∠C=78°, ∠EOD=90° и ∠FOD=168°.
Объяснение:
Не знаю, может и не правильно.
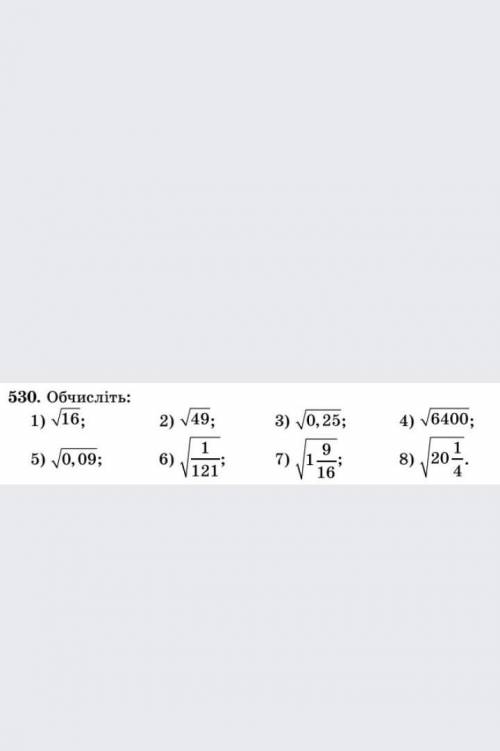
Объяснение:
1)4
2)7
3)0.5
4)80
5)0.3