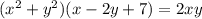
по примеру реши.
x^3 - 6x^2 + 11x - 6 = 0 можно, конечно, решить формулой кардано для решения кубических уравнений, но это долго и трудно. проще подобрать корни схемой горнера. возможные рациональные корни x = a/b, где а - делитель свободного члена, b - делитель старшего коэффициента. x = 1, -1, 2, -2, 3, -3, 6, -6 находишь значения в этих точках. y(1) = 1 - 6 + 11 - 6 = 0 - повезло сразу! теперь раскладываем: x^3 - x^2 - 5x^2 + 5x + 6x - 6 = 0 (x - 1)(x^2 - 5x + 6) = 0 (x - 1)(x - 2)(x - 3) = 0 ответ: x1 = 1, x2 = 2, x3 = 3
б) (6х -2)(2х - 1)= 12х(во 2-ой степени)-6х-4х+1= 12х(во 2-ой степени)-10х+1
в) (5х + 2у)(2х –3у)= 10х(во 2-ой степени)-15ху+4ху-6у(во 2-ой степени)= =10х(во 2-ой степени)-11ху-6у(во 2-ой степени)
г) (х +2)(х(во 2-ой степени)– 4х +7)= х(в 3-ей степени)-4х(во 2-ой степени)+7х+2х(во 2-ой степени)-8х+14= х(в 3-ей степени)-2х(во 2-ой степени)-х+14
2. а) 2х(х - 3) – 7(х - 3)=(х-3)(2х-7)
б) 2х + 2у + cx + cy= 2·(х+у)+с·(х+у)=(х+у)·(2+с)
3.а) - 0,3х(2х(во 2-ой степени)+ 3)(7 – 2х(во 2-ой степени))=( -0,6х(в 3-ей степени)-0,9)(7-2х(во 2-ой степени))= -4,2х(в 3-ей степени)+ 1,2х(в 5-ой степени)= -6,3+1,8х(во 2-ой степени)
б) 2с(3с – 4) – (с – 2)(с + 1)=6с(во 2-ой степени)-8с-(с(во 2-ой степени)+с- -2с-2)= 6с(во 2-ой степени)-8с-с(во 2-ой степени)-с+2с+2= 5с(во 2-ой степени)-7с+2
4.а) х(во 2-ой степени)+ ху – 2х -2у = (х(во 2-ой степени)-2х)+(ху-2у)= =х·(х-2)+у·(х-2)
б) кy –кх – yz + хz + х – y= (ку-yz-у)+(-кх+хz+х)= у·(к-z-1)-х·(к-z-1)= (к-z-1)(у+х)
5. 5а(а + в + с) – 5в(а – в – с) - 5с(а + в - с)= 5а(во 2-ой степени)+5ав+ +5ас-5ав+5в(во 2-ой степени)+5вс-5ас-5вс+5с(во 2-ой степени)= =5а(во 2-ой степени)+5в(во 2-ой степени)+5с(во 2-ой степени)