Объяснение:
у=х²+4х-2
Это парабола ,ветви вверх. Координаты вершины
а)х₀=-в/2а, х₀=(-4)/2=-2 , у₀=(-2)²+4*(-2)-2=-6 , (-2; -6).
б) во всех четвертях.
с) х=-2
d)Точки пересечения с осью ох, т.е у=0
х²+4х-2=0
Д=в²-4ас, Д=4²-4*4*(-2)=16+32=48=16*3
х₁=(-в+√Д):2а , х₁=(-4+4√3):2 , х₁=2(-2+2√3):2 , х₁=-2+2√3, (-2+2√3;0)
х₂=(-в-√Д):2а , х₂=(-4-4√3):2 , х₂=2(-2-2√3):2 , х₂=-2-2√3 , (-2-2√3;0)
Точки пересечения с осью оу, т.е. х=0, у=-2 (0;-2)
Доп.точки у=х²+4х-2 :
х: -5 -4 -3 1
у: 3 -2 -5 3
2)у=-х²-2х+6 Это парабола ,ветви вниз.
а)f(2)=-(2)²-2*2+6=-4-4+6=-2,
f(-2)=-(-2)²-2*(-2)+6=-4+4+6=6,
б) точка (-3;к) принадлежит графику функции, значит ее координаты удовлетворяют уравнению у=-х²-2х+6.
к=-(-3)²-2*(-3)+6 , к=-9+6+6 , к=3
a) Вероятность взять один синий карандаш, равна 5/9. В коробке останется 8 карандашей. Вероятность взять второй синий карандаш, равна 4/8 = 1/2, вероятность взять третий сини карандаш равна 3/7. По теореме умножения, 5/9 * 1/2 * 3/7 = 5/42
Аналогично вероятность взять один красный карандаш равна 4/9, второй красный карандаш - 3/8, третий красный карандаш - 2/7. По теореме умножения, 4/9 * 3/8 * 2/7 = 1/21
По теореме сложения, вероятность взять 3 карандаша одинакового цвета равна 5/42 + 1/21 = 5/42 + 2/42 = 7/42 = 1/6
б) Всего всевозможных исходов: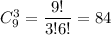 
из них нужно взять 2 синих и 1 красный карандаш, таких у нас 
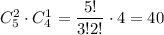. Вероятность того, что среди отобранных 3 карандаша 2 синих и 1 красный карандаш, равна 40/84 = 10/21
c) Вероятность того, что среди наугад выбранных 3 карандаша нет синего цвета, равна 1/21 (посчитали в пункте а), тогда вероятность того, что среди них будет хотя бы 1 карандаш синий, равна 1 - 1/21 = 20/21
y¹=1/3*3x²+1/2*2x+0=x²+x