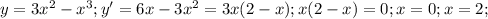Алгебра: Представьте в виде многочлена: а) 6x (х – 3) – х (2 - x); в) б) -а? (3а – 5) + 4а (а? — а); г)

1) - две критические точки в области определения R. 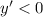на промежутках 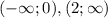и 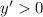на промежутке 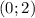, значит функция 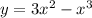убывает на промежутках 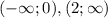и возрастает на промежутке 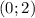. 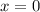- точка минимума, 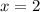- точка максимума. 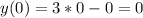- значение минимума функции, 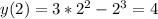- значение максимума функции.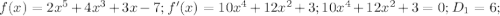 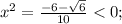2) - корней нет, 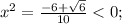- корней нет. 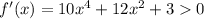итак, критических точек нет, значит в области определения R функция монотонна, т к при любых х, то функция 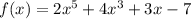возрастает в области определения R.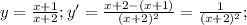 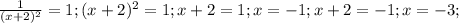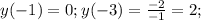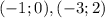3) т к касательная параллельна прямой у=х-3, то угловой коэффициент...

Представьте в виде многочлена: а) 6x (х – 3) – х (2 - x); в)
б) -а? (3а – 5) + 4а (а? — а); г)

👇

Увидеть ответ

Открыть все ответы

Ответ:

ангел769

09.12.2020

Задание № 1:

Найдите последнюю ненулевую цифру значения произведения 40^50*50^40?

$40^{50}*50^{40}=4^{50}*10^{50}*5^{40}*10^{40}=
(2^2)^{50}*5^{40}*10^{50}*10^{40}= \\ =2^{100}*5^{40}*10^{90}
=2^{60}*2^{40}*5^{40}*10^{90} = \\ =2^{60}*10^{40}*10^{90}=2^{60}*10^{130}$

10^130 нас не интересует. Попробуем повозводить 2 в степень:

2^1=2, 2^2=4, 2^3=8, 2^4=16, 2^5=32

Пятая степень, как и первая, оканчивается на 2. Образуется своего рода цикл.

Чтобы узнать последнюю цифру степени N, нужно N разделить на 4. Остаток от деления соответствует степени, последняя цифра которой совпадает с последней цифрой степени N. Остаток 0 соответствует 4-ой степени.

60/4=15, остаток 0 – 4 степень оканчивается на 6, значит и 60 степень оканчивается на 6

ОТВЕТ: 6

Задание № 3:

Сколько корней имеет уравнение: |x|=|x−1|+x−3?

$|x|=|x-1|+x-3
\\ \left\{\begin{array}{l} -x=-x+1+x-3, x\ \textless \ 0 \\ x=-x+1+x-3,0 \leq x
\leq 1 \\ x=x-1+x-3,x\ \textgreater \ 1 \end{array}$
$\left\{\begin{array}{l} 0=1+x-3, x\
\textless \ 0 \\ x=+1-3,0 \leq x \leq 1 \\ 0=x-1-3,x\ \textgreater \ 1
\end{array} \\ \left\{\begin{array}{l} x=2, x\ \textless \ 0 \\ x=-2,0 \leq x
\leq 1 \\ x=4,x\ \textgreater \ 1 \end{array}$

Условию раскрытия модуля соответствует только третья строчка.

ОТВЕТ: 1

4,6(15 оценок)

Ответ:

буду1

09.12.2020

y=3x^2-x^3; y'=6x-3x^2=3x(2-x);x(2-x)=0;x=0;x=2;

- две критические точки в области определения R.

на промежутках $(- \infty;0),(2;\infty)$ и y'0

на промежутке (0;2)

, значит функция y=3x^2-x^3

убывает на промежутках $(- \infty;0),(2;\infty)$ и возрастает на промежутке (0;2)

- точка минимума, x=2

- точка максимума. y(0)=3*0-0=0

- значение минимума функции, y(2)=3*2^2-2^3=4

- значение максимума функции.
2) f(x)=2x^5+4x^3+3x-7;f'(x)=10x^4+12x^2+3;10x^4+12x^2+3=0;D_1=6;

$x^{2} = \frac{-6- \sqrt{6}}{10}$ - корней нет,
$x^{2} = \frac{-6+\sqrt{6}}{10}$ - корней нет.
итак, критических точек нет, значит в области определения R функция монотонна, т к f'(x)=10x^4+12x^2+30

при любых х, то функция f(x)=2x^5+4x^3+3x-7

возрастает в области определения R.
3) т к касательная параллельна прямой у=х-3, то угловой коэффициент касательной k=1.
$y= \frac{x+1}{x+2}; y'= \frac{x+2-(x+1)}{(x+2)^2}=\frac{1}{(x+2)^2};$
$\frac{1}{(x+2)^2}=1;(x+2)^2=1;x+2=1;x=-1;x+2=-1;x=-3;$
$y(-1)=0;y(-3)= \frac{-2}{-1}=2;$
(-1;0),(-3;2)