ответы на эти вопросы я уже знаю так то решил Вам) Тема: Квадратичные функции вида y = a(x – m)², y = ax² + n и y = a(x – m)² + n при a ≠ 0, их графики и свойства. Урок 1
1. Путем сдвига вдоль оси ОХ на 3 единицы влево
2. Область определения функции (–∞; +∞),
График функции проходит через точку (2; 128)
3. ответ 3. g(x) = (x – 3)2.
4. Единицы в право и вверх
5.График функции проходит через точку (2; 7)
Промежуток возрастания x ∈ [0; +∞)
Область определения функции (–∞; +∞)
6. 1-4, 2-1, 3-2, 4-3, 5-5
7. 1-4, 2-1, 3-2, 4-3
8. Промежуток возрастания x ∈ [5; +∞)
Множество значений функции [15; +∞)
(Смог найти только 2)
9. 1-4, 2-1, 3-2, 4-3, 5-5
Надеюсь
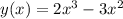
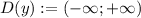
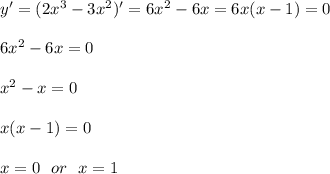
![+++++++[0]---------[1]+++++++\ \textgreater \ x](/tpl/images/0905/2664/fbfbf.png)
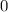 являеться максимумом функции
являеться максимумом функции 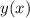 ,
, являеться минимумом функции
являеться минимумом функции 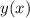
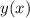 монотонно растет на промежутке
монотонно растет на промежутке 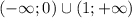
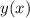 монотонно убывает на промежутке
монотонно убывает на промежутке 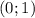
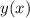 пересекает ось ОХ в точкаx
пересекает ось ОХ в точкаx 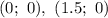
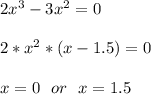
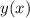 пересекает ось ОУ в точке
пересекает ось ОУ в точке 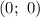
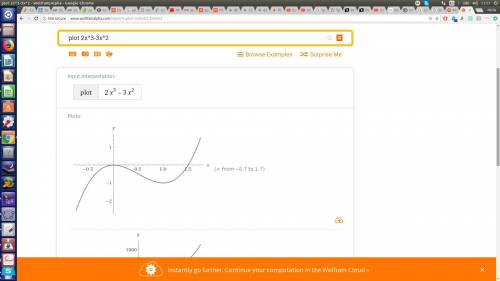
ищем критические точки:
смотрим, как ведет себя производная функции при переходе через эти точки:
производная в точке 0 меняет знак с + на - , что означает, что точка
производная в точке 1 меняет знак с - на + , что означает, что точка
----------------
тогда промежутки монотонности:
ф-ия
ф-ия
----------------
ф-ия
ф-ия
на основании этих данных и строиться схематический график