у = kx + b
так как график проходит через начало координат, b = 0.
подставим координаты точки М в уравнение
4 = k * (-2.5)
Отсюда найдем k = 4/(-2.5) = -1.6
то есть искомая формула линейной функции у = -1,6х
Теперь, чтоб найти точку пересечения этого графика с прямой 3х-2у - 16 = 0, решим систему из 2 линейных уравнений
у = -1,6х
3х-2у - 16 = 0
подставив у из первого уравнения во второе, получим
3х + 3,2х - 16 = 0
6,2х = 16
х = 16/6,2= 80/31
тогда у = -1,6 *80/31 = -128/31
То есть искомая точка пересечения (80/31; -128/31)
а) b = 18 б) b = 10 в) y=20 г) y = 1,2
д) a = 9 е) a = 24 ж) x = 1,4 з) x = 0,6
Объяснение:
Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних членов пропорции.
a : b = c : d ⇒ ad = bc
а) 2 : 9 = 4 : b; 2b = 9*4; 2b = 36; b = 36 : 2; b = 18;
б) 15 : b = 3 : 2; 15*2 = b*3; 30 = 3b; b = 30 : 3; b = 10;
в) 3 : 2,1 = y : 14; 3 * 14 = 2,1y; 42 = 2,1y; y = 42 : 2,1; y = 20;
г) y : 2,4 = 3 : 6; 6y = 2,4*3; 6y = 7,2; y = 7,2 :6; y = 1,2;
д) 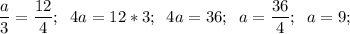
е) 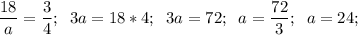
ж) 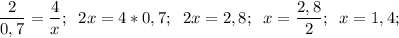
з) 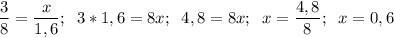
Задание удобно решать графически.Надо начертить график ф-ции у=|x-1|+|x+1| и у=а.
Знаки |x-1| - - - (-1) - - - (1) + + +
Знаки |x+1| - - - (-1) + + + (1) + + +
Рассматриваем три интервала.
-∞<х≤ -1 ⇒ у=-х+1-х-1=-2х Строим эту прямую y=-2x при х∈(-∞,-1].
-1<x≤1 ⇒ y=-x+1+x+1=2 ⇒Прямую у=2 строим при х∈(-1,1]
1<х<∞ ⇒у=х-1+х+1=2х . Строим прямую у=2х при х∈(1,∞)
Прямые строят только в тех пределах изменения переменной х, в которой это указано.Остальные части прямых стирают.
По графику будет видно, что прямая у= а,которая параллельна оси ОХ не будет перес екать график ф-ции у=|x-1|+|x+1| при а<2.А значит, при а<2 уравнение не имеет корней