2cos(π/3 - 3x) + √3 = 0
2cos(π/3 - 3x) = -√3
cos(π/3 - 3x) = -√3/2
• Воспользуемся формулой:
cos(x) = b ( |b|≤ 1, [0; π] )
x = ± arccos(b) + 2πn, n ∈ ℤ
• Получаем:
cos(π/3 - 3x) = -√3/2
π/3 - 3x = ± arccos(-√3/2) + 2πn, n ∈ ℤ
π/3 - 3x = ± (π - arccos(-√3/2)) + 2πn, n ∈ ℤ
π/3 - 3x = ± (π - 5π/6) + 2πn, n ∈ ℤ
π/3 - 3x = ± π/6 + 2πn, n ∈ ℤ
-3x = ± π/6 - π/3 + 2πn, n ∈ ℤ
[ -3x = -π/6 - π/3 + 2πn, n ∈ ℤ
[ -3x = π/6 - π/3 + 2πn, n ∈ ℤ
[ -3x = -π/2 + 2πn, n ∈ ℤ / : (-3)
[ -3x = -π/3 + 2πn, n ∈ ℤ / : (-3)
[ x = π/6 - 2πn/3, n ∈ ℤ
[ x = π/9 - 2πn/3, n ∈ ℤ
ответ: x = π/6 - 2πn/3, n ∈ ℤ ; x = π/9 - 2πn/3, n ∈ ℤ
.
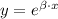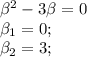
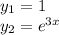
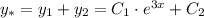
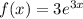
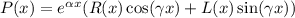, где R(x) и S(x) - полиномы, которое имеет частное решение.
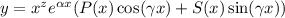, где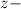 
кратность корня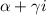 
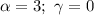
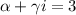является корнем характеристического уравнения кратности z=1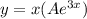
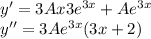
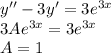
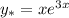
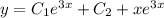
ответ: 0
Объяснение:
(3a+ 1)(9a²- 3a + 1) = 27a³+1 =27×(-1/3)³ + 1 = - 27×1/27 + 1 = -1 + 1 = 0