247/16-х время против течения
247/16+х время по течению, оно на 6ч меньше, чем время против течения.
Составляем уравнение и решаем его
247/16-х - (247/16+х)=6 приводим к общему знаменателю(16+х)(16-х), получаем
247(16+х ) - 247(16-х) = 6(16+х)(16-х)=6(256-х²)
247(16+х-16+х)=1536-6х²
247*2х=1536-6х²
делим на 2
247х=768-3х²
3х²+247х-768=0
Находим корни квадратного уравнения , получаем
Х₁=( -247- √ 2472+4*3*768):2*3= (-247-265):6= отриц.число, скорость течения не может быть отриц. По модулю
Х₂=( -247+ √ 2472+4*3*768):2*3= (-247+265):6=18:6=3 км/ч
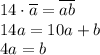
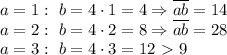
а + b + с = 2 (1)
Решение квадратного урвнения х = 2 подставим в уравнение
ax²+bx+c=0
4а +2b +с = 0 (2)
единственное решение имеет место, если дискриминант квадратного уравнения ax²+bx+c=0 равен нулю
D = b² - 4ac
b² - 4ac = 0 (3)
Из (1) выразим а = 2 - b - c (1a)
Из (2) выразим c = -4a -2b (2a)
Подставим (1а) в (2а)
c = -4(2 - b - c ) - 2b
c = -8 + 4b + 4c - 2b
-3c = -8 + 2b
c = (8 - 2b):3 (4)
Подставим (4) в (1а)
а = 2 - b - (8 - 2b):3
а = (-2 - b):3 (5)
Подставим (4) и (5) в (3)
b² - 4·((-2 - b):3)·((8 - 2b):3) = 0
9b² + 4·(2 + b)·(8 - 2b) = 0
9b² + (8 + 4b)·(8 - 2b) = 0
9b² + 64 + 32b -16b - 8b² = 0
b² + 16b + 64 = 0
(b + 8)² = 0
b = -8
подставим b в (4) и (5)
c = (8 - 2·(-8)):3 = 8
а = (-2 - (-8)):3 = 2
ответ: а = 2, b = -8, с = 8