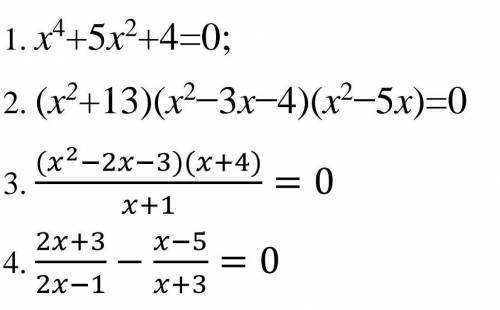
(см. объяснение)
Объяснение:
Я так понимаю, нужно объяснить разложение на множители.
Сделать это не так сложно.
Вот пример:
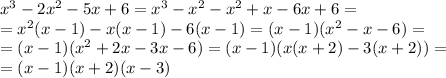
Откуда такие преобразования?
Напишу универсальный алгоритм:
По теореме Безу определить корень уравнения (если корень целый, то он обязательно будет делителем свободного члена (того, что без x)). В нашем один из корней корень x=1.По схеме Горнера или уголком поделить исходный многочлен на x-a, где a - корень уравнения (в нашем случае 1), т.е. делим на (x-1).В результате деления получим (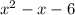
). Первый этап выполнен. Сейчас имеем 
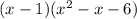.Если уравнение не квадратное, идем на первый этап. Иначе идем на этап 5.Решим уравнение 
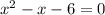(решается либо через дискриминант, либо через теорему Виета). Корни 
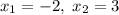.Вспомним формулу: 
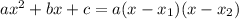. Здесь 
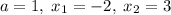. Тогда: 
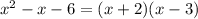.Получили результат: 
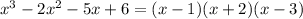.Разложение на множители выполнено!
( 8 * ( 12 + 18 ) ) : ( 3 - 2 )
Объяснение:
Можно увеличить значение выражения, если умножить 8 на наибольшее число. Но также благодаря делению мы можем уменьшить значение, поэтому сразу делить - плохая идея. Стоит заметить, что в конце стоит -2, и поэтому мы сможем разделить на наименьшее из возможных чисел (ну, кроме нуля, конечно), т.е на (3-2) = 1.
Итого получаем: (8*12+18):(3-2)
Выгодней будет поставить скобки так (8*(12+18)):(3-2), потому что 18 > 12, и увеличивая число, на которое мы умножаем, мы максимально увеличили произведение.
Мы максимально уменьшили делитель и максимально увеличили делимое, следовательно - (8*(12+18)):(3-2) - наибольший из возможных вариантов.
хз
Объяснение: