Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2) 
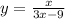. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б) 
при 
Если x = -5, то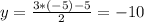 
Если х= 3, то 
Значит, 
Очень найдите ( sin5α + sinα , если sinα = 1/√5
"решение" : * * * sinα +sinβ =2sin( (α+β)/2 ) *cos( (α - β)/2 ) * * *
sin5α + sinα = 2*sin ( (5α +α)/2 ) *cos ( (5α -α)/2 ) =
2*sin3α*cos2α =2*(3sinα - 4sin³α)* (1 -2sin²α ) = || sinα = 1/√5 || =
=2*(3 /√5 - 4 / 5√5)* (1 - 2* 1/5 ) = 2*( ( 3*5 - 4) / 5√5 )*( (5*1 -2)5 ) =
=2* (11 / 5√5) * (3/5) = 66/25√5 = 66√5 / 125
ответ: 66√5 / 125
* * * P.S. sin3α =sin(2α+α) = sin2α*cosα+ cos2α*sinα =
2sinα*cosα*cosα + (cos²α -sin²α)*sinα =sinα *(2cos²α + cos²α - sin²α) =
sinα *(3cos²α - sin²α) = sinα *( 3(1 -sin²α) - sin²α ) = 3sinα - 4sin³α * * *
ответ: 2 км/час.
Объяснение:
Дано. Катер плыл 2,3 ч по течению
и 3,5 ч против течения.
Всего он проплыл 133,9 км.
Найдите скорость течения, если
собственная скорость катера 23,5 км/ч.
Решение.
Обозначим скорость течения через х км/час.
Тогда скорость катера по течению будет 23,5+х км/час
скорость против течения --- 23,5 - х км/час.
S=vt.
Путь по течению равен
S1= (23,5+х)2.3 = 54.05 +2.3x км.
Путь против течения равен
S2=(23.5-x)3.5 = 82.25-3.5x км.
Весь путь равен 133,9 км.
Составим уравнение:
54,05+2,3х + 82,25-3,5х = 133,9;
2,3х-3,5х = 133,9-54,05-82,25;
-1,2х=-2,4;
х=2 км/час - скорость течения реки.