
Пусть t(ч) — время, за которое Пончик съедает три плюшки, x(км/ч) — скорость автобуса. В момент времени, когда мимо Пончика проехал автомобиль, автобус находился от него на расстоянии 2xt км, а мотоцикл — на расстоянии 30t км. Cпустя a часов, в тот момент времени, когда мимо Сиропчика проехал мотоцикл, автомобиль находился от него на расстоянии 60t км, а автобус — на расстоянии 2xt км от мотоцикла, следовательно, на расстоянии 2xt – 60t км от автомобиля. Сравнивая расстояния, пройденные автомобилем и мотоциклом получаем уравнение a(60 – 30) = 60t + 30t, откуда , а сравнивая расстояния, пройденные автобусом и автомобилем, получаем уравнение a(60 – x) = (2xt – (2xt – 60t)) = 60t, откуда .
ответ: 40 км/ч.
5,72
1) (x+y) * (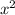 - xy +
- xy + 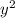 )
)
2) (x-y) * (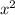 + xy +
+ xy + 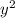 )
)
3) (m-n) * (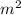 + mn +
+ mn + 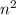 )
)
4) (m+n) * (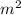 - mn +
- mn + 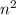 )
)
5) (p+q) * ( - pq +
- pq + 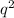 )
)
6) (p-q) * ( + pq +
+ pq + 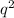 )
)
7) (a+2) * (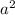 -2a + 4)
-2a + 4)
8) (a-2) * (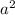 + 2a + 4)
+ 2a + 4)
9) (m+3) * (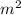 - 3m + 9)
- 3m + 9)
5.73
1) (3-2a) * (9 + 6a + 4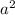 )
)
2) (2x+y) * (4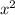 - 2xy +
- 2xy + 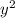 )
)
3) (3a-2b) * ( 9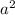 + 6ab + 4
+ 6ab + 4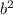 )
)
4) (1+4y) * ( 1 - 4y + 16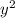 )
)
5) (5x-3y) * (25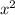 + 15xy + 9
+ 15xy + 9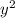 )
)
6) (1 -2a) * ( 1 + 2a + 4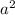 )
)