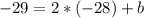
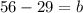
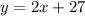
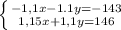
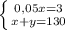
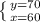
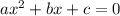 где коэффициенты
где коэффициенты 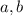 и
и  соответственно
соответственно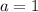 ,
, 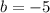 и
и 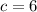
 при
при 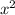 равен 1, единица больше 0, сл, ветви параболы будут направлены вверх
равен 1, единица больше 0, сл, ветви параболы будут направлены вверх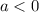 ветви будут направлены вниз)
ветви будут направлены вниз) обозначается как
обозначается как 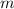 и считается по формуле
и считается по формуле 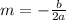
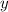 обозначается
обозначается 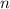 и ищется путем подстановки числа
и ищется путем подстановки числа 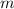 в уравнение вместо
в уравнение вместо 
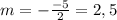
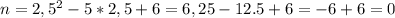
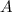 вершины параболы имеет координату (2,5;0)
вершины параболы имеет координату (2,5;0)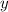
 и
и 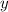
 находятся при, при
находятся при, при 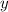 = 0
= 0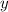 - когда
- когда  = 0
= 0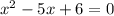
 то есть 6
то есть 6 в уравнение и найти относящиеся к ним
в уравнение и найти относящиеся к ним 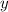 - это и будут координаты точек, через которые проходит график
- это и будут координаты точек, через которые проходит график
Одночлены можно сложить с приведением подобных членов в случае, если буквенная часть одинакова, а коэффициенты (числовые множители перед буквенной частью ) различные.
Действуем по правилу сложения подобных слагаемых. Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Например, из того, что написано:
Если одночлены не подобны, то упрощение суммы не получится, а останется многочлен, то есть сумма нескольких одночленов. Например, сумма одночленов
А вот пример, где можно немного упростить сумму одночленов.