2x-3y=11
5x+y=2
Данную систему уравнений можно решить двумя
подстановки
извлекаем из второго уравнения у:
у=2-5х
и подставляем это выражение в первое выражение заместо у:
2х-3(2-5х)=11
2х-6+15х=11
Решаем простое линейное уравнение:
17х=17
х=1
Теперь находим значение у:
у=2-5*1
у= -3.
А теперь я решу эту систему методом сложения:
2х-3у=11
5х+у=2
Домножу на 3 второе уравнение:
2х-3у=11
15х+3у=6
17х=17
х=1
Теперь,чтобы найти значение у,нужно в любое из двух уравнений подставить значение х=1. После подставновки получаем, что у= -3
ответ получается один и тот же,несмотря каким ты решаешь)
ответ: (1; -3)
![1. \sqrt[3]{5x+7}-\sqrt[3]{5x-12}=1](/tpl/images/0647/5689/e0f48.png)
делаем замену:
![\sqrt[3]{5x+7}=a \\\sqrt[3]{5x-12}=b](/tpl/images/0647/5689/6c3de.png)
избавляемся от корня:
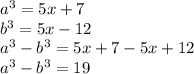
составляем систему и решаем ее:
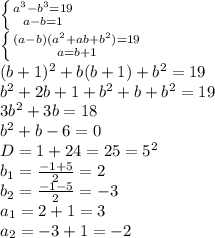
подставляем значения a и b:
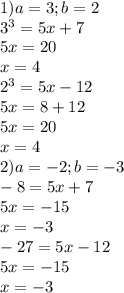
В итоге получили два корня: -3 и 4
ответ: 4; -3
следущее уравнение решается аналогично.
![2. \sqrt[3]{x+6}+\sqrt[3]{66-x}=6\\\sqrt[3]{x+6}=a\\\sqrt[3]{66-x}=b\\a^3=x+6\\b^3=66-x\\a^3+b^3=72\\\left \{ {{a^3+b^3=72} \atop {a+b=6}} \right. \\\left \{ {{(a+b)(a^2-ab+b^2)=72} \atop {a+b=6}} \right. \\\left \{ {{a^2-ab+b^2=12} \atop {a=6-b}} \right. \\(6-b)^2-b(6-b)+b^2=12\\(b-6)^2+b(b-6)+b^2=12\\b^2-12b+36+b^2-6b+b^2=12\\3b^2-18b+24=0\\b^2-6b+8=0\\D=36-32=4=2^2\\b_1=\frac{6+2}{2} =4\\b_2=\frac{6-2}{2} =2\\a_1=6-4=2\\a_2=6-2=4](/tpl/images/0647/5689/4b08e.png)
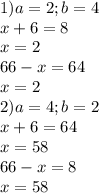
ответ: 58; 2
![3. \sqrt{x+2}-\sqrt[3]{3x+2}=0\\\sqrt{x+2}=\sqrt[3]{3x+2}=0](/tpl/images/0647/5689/cc477.png)
возводим обе части в шестую степень:
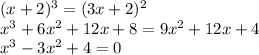
не забываем, что по определению арифмитического квадратного корня:
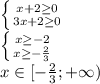
продолжаем решать уравнение:
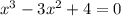
корнями данного уравнения могут быть делители свободного члена:
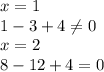
один из корней уравнения: x=2
значит данное уравнение можно представить в виде произведения (x-2) на квадратный трехчлен:
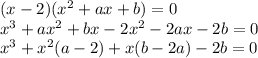
приравняем коэффициенты:
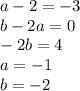
получим:
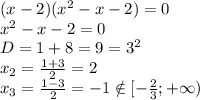
ответ: 2
решение на фотографии