(x^4-2x^2-8):(x^2+2x+1)<0 заметим что знаменатель x^2+2x+1=(x+1)^2 больше равен 0 (при х=-1 знаменатель=0 ) значит знаменатель можно отбросить и смотреть когда числитель <0 x^4-2x^2-8<0 (x≠-1) x^4-2x^2+1-1-8<0 x^4-2x^2+1-9<0 (x^2-1)^2-3^2<0 (x^2-4)(x^2+2)<0 второй член всегда больше 0 значит x^2-4<0 (x-2)(x+2)<0 (-2) (2) ответ (-2 -1) U ( -1 2)
1 < (3x^2-7x+8):(x^2+1)<2 x^2+1 всегда больше 0 значит можно умножить левуб и правую часть на положительное число (x^2+1) < (3x^2-7x+8)<2(x^2+1) (x^2+1) < (3x^2-7x+8) 0< 2x^2-7x+7 D=7^2-4*2*7=49-56<0 дискриминант <0 и коэффициент при квадрате больше 0 значит это выражение всегда больше нуля рассмотрим второе (3x^2-7x+8)<2(x^2+1) x^2-7x+6<0 D=49-24=25 x12=(7+-5)/2=1 6 (x-1)(x-6)<0 1 6 x∈ (1 6)
Объяснение:
х км/ч - скорость катера в стоячей воде;
(x-2) км/ч - скорость катера против течения;
(x+2) км/ч - скорость катера по течению;
20/(x+2) ч - время, пройденное по течению;
8/(x-2) ч - время, пройденное против течения.
На весь путь катер затратил 2 часа, составим уравнение
Домножив обе части уравнения на 0.5(x+2)(x-2), получаем
10(x-2) + 4(x+2) = (x+2)(x-2)
10x - 20 + 4x + 8 = x² - 4
x² - 14x + 8 = 0
D = 14² - 4 * 1 * 8 = 164
Корень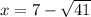 не удовлетворяет условию.
не удовлетворяет условию.