Объяснение:
выражение в квадратном корне должно давать положительный результат, иначе выражение не
имеет смысла
1) √х. х не должен быть –1 или каким-то другим отрицательным числом, поэтому выражение имеет смысл при х (0; +∞)
2) √х². Здесь х также может быть и отрицательным, поскольку он возведён во вторую степень, которая даёт положительный результат в любом случае поэтому: х (–∞; +∞)
3) √–х. х не должен быть положительным, поскольку при положительном х у нас получится отрицательный итог, например при х=1 =√–1, это недопустимо, поэтому х должен быть: х≤0 и значение следующие: х (–∞; 0)
5) √25х. х должен быть 0 или положительное значение:
х≥0, поэтому х (0; +∞)
4) √–3х. х должен быть отрицательным, чтобы выражение давало положительный результат:
х (–∞; –1)
6) √0,01х, х≥0; х (0; +∞)
7)
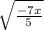
х ≥ 0; х (–∞; 0)
8)
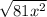
х может быть как положительным так и отрицательным, поскольку он возведён во вторую степень и значение выражения всегда будет положительным: х (–∞; +∞)
Объяснение:
выражение в квадратном корне должно давать положительный результат, иначе выражение не
имеет смысла
1) √х. х не должен быть –1 или каким-то другим отрицательным числом, поэтому выражение имеет смысл при х (0; +∞)
2) √х². Здесь х также может быть и отрицательным, поскольку он возведён во вторую степень, которая даёт положительный результат в любом случае поэтому: х (–∞; +∞)
3) √–х. х не должен быть положительным, поскольку при положительном х у нас получится отрицательный итог, например при х=1 =√–1, это недопустимо, поэтому х должен быть: х≤0 и значение следующие: х (–∞; 0)
5) √25х. х должен быть 0 или положительное значение:
х≥0, поэтому х (0; +∞)
4) √–3х. х должен быть отрицательным, чтобы выражение давало положительный результат:
х (–∞; –1)
6) √0,01х, х≥0; х (0; +∞)
7)
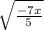
х ≥ 0; х (–∞; 0)
8)
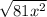
х может быть как положительным так и отрицательным, поскольку он возведён во вторую степень и значение выражения всегда будет положительным: х (–∞; +∞)
Вероятность выигрыша 0,5, значит вероятность проигрыша 1-0,5=0,5
Найти количество билетов чтобы вероятность выигрыша была
не менее 0,999
Решим альтернативную задачу: найдем количество билетов, чтобы вероятность проигрыша была менее 0,001
первый билет проиграл 0,5
значит берем второй билет и он тоже проиграл 0,5*0,5=0,25>0.001
значит берем третий билет и он тоже проиграл 0,25*0,5=0,125>0.001
четвертый 0,125*0,5=0,0625>0,001
пятый 0,0625*0,5=0,03125>0.001
шестой 0,03125*0,5=0,015625>0,001
седьмой 0,015625*0,5=0,0078125>0.001
восьмой 0.0078125*0.5=0.00390625>0,001
девятый 0,0039*0,5=0,00195>0.001
десятый 0.00195*0.5=0.00097 <0.001
Значит среди 10 билетов хотя бы один будет выигрышный