(2х-5)(3х+4)=6x^2+8x-15x-20=6x^2-7x-20
(х-3у)(2у-5х)=2xy-5x^2-6y^2+15xy=-5x^2+17xy-6y^2
а(а-5)-(а-2)(а-3)=a^2-5a-a^2+3a+2a-6=-6
(2b+1)(4b^2-2b+1)=8b^3-1
х^3+2х^2+х+2=x(x^2+1)+2(x^2+1)=(x+2)(x^2+1)
4х-4у+ху-у^2=4(x-y)+y(x-y)=(4+y)(x-y)
№3
2х^2(4х^2-3)(3+4х^2)=32х^6-18х^2
(8x^4-6x^2)(3+4x^2)=32x^6-18x^2
24x^4+32x^6-18x^2-24x^2=32x^6-18x^2 24x^4-24x^4=0
32x^6-18x^2=32x^6-18x^2
№4
а^2-bc+ab-ac=a(a-c)+b(a-c)=(a+b)(a-c)
3а+ab^2-а^2b-3b=3(a-b)-ab(a-b)=(3-ab)(a-b)
№5
x-2=y+1 x=y+3
(x-2)(y+1)=xy-4
(y+1)(y+1)=y^2+3y-4
y^2+2y-y^2-3y=-5 y^2-y^2=0
-y=-5
y=5
x=y+3
x=5+3
x=8
проверка
y+1=5+1=6
x-2=8-2=6
6*6=36 5*8=40
40-36=4
сторона квадрата равно 6
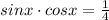
![[-\pi;\pi]](/tpl/images/0144/2399/fdb8f.png)
Чтобы решить это уравнение, нужно привести к одной функции (т.е. чтобы либо только cos, либо только sin)
Вспоминаем формулу синуса двойного угла: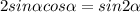 
Она бы нам подошла, если бы слева перед синусом и косинусом стояла двойка. Так как ее нет, мы подгоняем:
Эти уравнения совершенно равнозначны: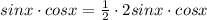 
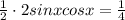
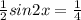
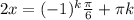
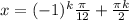
Это общее уравнение, а нам нужны корни на заданном промежутке. Промежуток ![[-\pi; \pi]](/tpl/images/0144/2399/0c866.png)
для удобства можем представить как ![[\frac{-12 \pi}{12}; \frac{12 \pi}{12}]](/tpl/images/0144/2399/c0238.png)
. Так удобнее для сравнения. Делаем выборку, подставляя вместо k разные целые числа: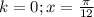
- этот корень принадлежит данному промежутку
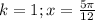-принадлежит
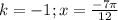- принадлежит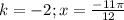
Получилось что 4 корня принадлежат.
ответ: 4
2(3x+1)+3(6y-1)=7
(3x+1)-3(6y-1)=8
2(3x+1)+3(6y-1)=7
6x+2+18y-3-7=0
6x-8+18y=0
y=(-6x+8)/18
(3x+1)-3(6y-1)=8
3x+1-18y+3-8=0
3x-4-18y=0
3x-4-18*((-6x+8)/18)=0
3x-4-(-6x+8)=0
9x-12=0
x=12/9
x=4/3
6x-8+18y=0
6*4/3-8+18y=0
18y=0
y=0