
Рассмотрим произвольный прямоугольный треугольник АВС и проведем высоту СН = h из вершины С его прямого угла. Она разобьет данный треугольник на два прямоугольных треугольника АСН и ВСН; каждый из этих треугольников имеет с треугольником АВС общий острый угол и потому подобен треугольнику АВС. Все три треугольника АВС, АСН и ВСН подобны между собой. Из подобия треугольников АВС и АСН имеем СН2 = АН×ВН, т.е.
Теорема. Высота прямоугольного треугольника, опущенная из вершины прямого угла на гипотенузу, равна среднему геометрическому отрезков, на которые она разбивает гипотенузу.
h^2=m*n
a^2=c*m
b^2=c*n
c- гипотенуза
m и n - ее части
Чтобы достать оранженвый карандаш с вероятностью, большей 0,2, нужно, чтобы общее число карандашей было меньше 5/0,2=25 штук. Так как в коробке уже лежит 16 карандашей, то туда можно доложить менее 25-16=9 карандашей. Значит, максимальное число красных карандашей - 8 штук.
Если уравнением, то х - все карандаши, красные карандаши - y:
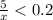
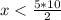
x<25
y<25-16
y<9
y=8.
ответ: 8 штук - наибольшее число красных карандашей, которые можно положить в коробку, чтобы после этого вероятность наугад достать из коробки оранжевый карандаш была больше 0,2. ;)
№166
1)x=-3 => y=9
x=4.5 => y=-6
x=0 => y=3
2)y=7 => x=-2
y=-3 => x=3
y=0 => x=1.5
№168
1)x=4 => y=3
x=-1 => y=-7
x=0.5 => y=-4
2)y=1 => x=3
y=-1 => x=2
y=0 => x=2.5
3)y>0 при xэ(2.5;+∞)
№170
1)x=8 => y=2
x=2 => y=0.5
x=-4 => y=-1
x=-3 => y=-0.75
2)y=-2 => x=-8
y=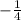 => x= -1
=> x= -1
y=0 => x= 0
y=16 => x= 64
№172
1)x=4 => y=6
x=-2 => y=-3
2)y=-3 => x=-2
y=4.5 => x=3