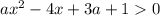
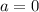 квадратное неравенство вырождается в линейное
квадратное неравенство вырождается в линейное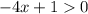
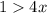
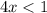
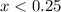
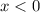
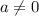
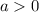
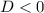 ) - отлично, график параболы выше оси Ох - неравенство выполняется
) - отлично, график параболы выше оси Ох - неравенство выполняется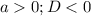
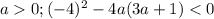
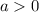

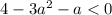
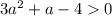
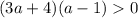
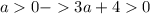 авмтоматически
авмтоматически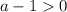 или
или 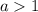
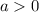 -
- 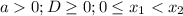 ;
; 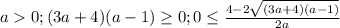
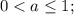 - с первых двух неравенств (аналогично по рассуждениям относительно первого случая)
- с первых двух неравенств (аналогично по рассуждениям относительно первого случая)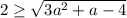
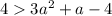
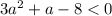 - что очевидно верно при условиях
- что очевидно верно при условиях 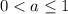
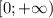
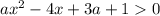
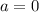 квадратное неравенство вырождается в линейное
квадратное неравенство вырождается в линейное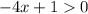
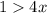
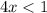
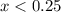
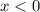
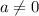

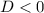 ) - отлично, график параболы выше оси Ох - неравенство выполняется
) - отлично, график параболы выше оси Ох - неравенство выполняется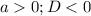
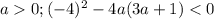

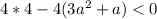
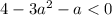
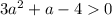
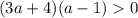
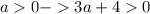 авмтоматически
авмтоматически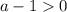 или
или 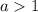
 -
- 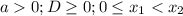 ;
; 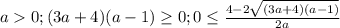
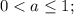 - с первых двух неравенств (аналогично по рассуждениям относительно первого случая)
- с первых двух неравенств (аналогично по рассуждениям относительно первого случая)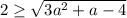
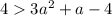
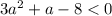 - что очевидно верно при условиях
- что очевидно верно при условиях 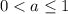
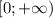
Формула суммы n первых членов арифметической прогрессии: Sn = (а1 + аn)*n/2.
a1 = 1, а20 = 20 (Для натуральных чисел - сам элемент соответствует его номеру.
S20 = (a1 + a20)*20/2 = (1 + 20)*20/2 = 21*20/2 = 210.
ответ: 210.