

Против течения катер шел расстояние Х
А по течению Х+32
Х+Х+32=88
2Х=56
Х=28
Получается,что катер против течения за 2 часа 28 км
С какой скоростью шёл катер
28:2=14 километров в час
Сколько километров катер по течению
28+32=60
Теперь ответим на вопрос,если бы катеру не течение,то сколько км он бы за 3 часа
14•3=42,а на самом деле км
Найдём разницу
60-42=18 км
Значит благодаря течению катер на 18 км больше за 3 часа
Теперь узнаём скорость течения
18:3=6
Скорость катеру по течению была 20 километров в час
60:3=20 км/час или 14+6=20 км/час
ответ:Скорость течения реки 6 км/час
Скорость катера в стоячей воде 24 ем/час
Скорость катера по течению 20 км/час
Объяснение:
В решении.
Объяснение:
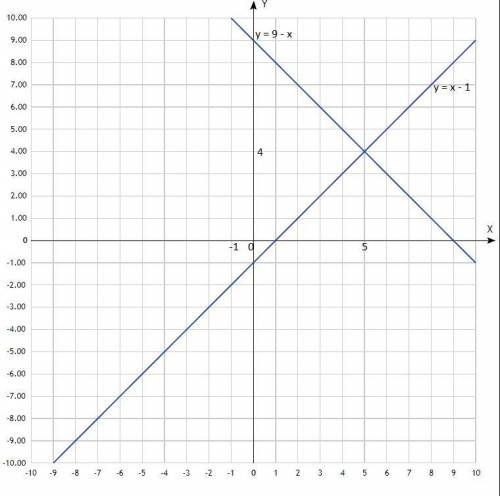
Решить графически систему уравнений:
у = 9 - х
у = х - 1
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у = 9 - х у = х - 1
Таблицы:
х -1 0 1 х -1 0 1
у 10 9 8 у -2 -1 0
Координаты точки пересечения прямых: (5; 4).
Решение системы уравнений: (5; 4).
1.
а) (6a² + 9a) - (a² - 5 + 9a) = 6a² + 9a - a² + 5 - 9a = 5a² + 5 = 5(a² + 1)
б) 6a⁴ - 2a²(3a² + 7) = 6a⁴ - 6a⁴ - 14a² = -14a²
2.
а) 10xy + 15y² = 5y(2x + 3y)
б) 2y⁴ - 6y⁷ = 2y⁴(1 - 3y³)
3.
а) x² - 4x = 0
x(x - 4) = 0
Уравнение имеет два корня, найдем каждый:
x₁ = 0
x₂ - 4 = 0
x₂ = 4
4.
8x = 5y, когда y = x + 6
8x = 5(6 + x)
8x = 30 + 5x
3x = 30
x = 10
ответ: 10 деталей в час