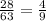
ответ: 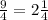
как найти точки пересечения графика функции с осями координат?
с осью абсцисс график функции может иметь любое количество общих точек (или ни одной). с осью ординат — не более одной (так как по определению функции каждому значению аргумента ставится в соответствие единственное значение функции).
чтобы найти точки пересечения графика функции y=f(x) с осью абсцисс, надо решить уравнение f(x)=0 (то есть найти нули функции).
чтобы найти точку пересечения графика функции с осью ординат, надо в формулу функции вместо каждого x подставить нуль, то есть найти значение функции при x=0: y=f(0).
примеры.
1) найти точки пересечения графика линейной функции y=kx+b с осями координат.
решение:
в точке пересечения графика функции с осью ox y=0:
kx+b=0, => x= -b/k. таким образом, линейная функция пересекает ось абсцисс в точке (-b/k; 0).
в точке пересечения с осью oy x=0:
y=k∙0+b=b. отсюда, точка пересечения графика линейной функции с осью ординат — (0; b).
например, найдём точки пересечения с осями координат графика линейной функции y=2x-10.2x-10=0; x=5. с ox график пересекается в точке (5; 0).
y=2∙0-10=-10. с oy график пересекается в точке (0; -10).
2) найти точки пересечения графика квадратичной функции y=ax²+bx+c с осями координат.
решение:
в точке пересечения графика с осью абсцисс y=0. значит, чтобы найти точки пересечения графика квадратичной функции (параболы) с осью ox, надо решить квадратное уравнение ax²+bx+c=0.
в зависимости от дискриминанта, парабола пресекает ось абсцисс в одной точке или в двух точках либо не пересекает ox.
в точке пересечения графика с осью oy x=0.
y=a∙0²+b∙0+c=с. следовательно, (0; с) — точка, в которой парабола пересекает ось ординат.
например, найдём точки пересечения с осями координат графика функции y=x²-9x+20.
x²-9x+20=0
x1=4; x2=5. график пересекает ось абсцисс в точках (4; 0) и (5; 0).
y=0²-9∙0+20=20. отсюда, (0; 20) — точка пересечения параболы y=x²-9x+20 с осью ординат.
Пусть первая пропускает х литров воды в минуту, тогда вторая х+4.
у - время, за которое первая труба заполняет резервуар в 480 литров, тогда
(у-8) - время, за которое вторая труба заполняет резервуар в 384 литра.
Получается система уравнений:
ху = 480; (х+4)(у-8) = 384
х = 480/у; ху - 8х + 4у - 32=384;
х = 480/у; (подставляем во второе уравнение системы:)
480*у/у - 8*480/у + 4у - 32 - 384 = 0
480 - 3840/у + 4у - 416 = 0 (умножаем обе части равенства на у
480у - 3840 + 4у^2 - 416у = 0
4у^2 + 64 у - 3840 = 0 (делим обе части равенства на 4
у^2 + 16у - 960 = 0
По формуле высчитываем дискриминант:
Д = 16*16 - 4*1*(-960) = 256 + 3840 = 4096
у1 = (-16 + 64)/2*1 = 24
у2 = отрицательное число О_О
х = 480/у = 480/ 24 = 20
ответ: первая труба пропускает 20 литров воды в минуту
²⁸/₆₃=⁴/₉
Обратное полученному ⁹/₄=2¹/₄