(c+1)-c2
7(х+8)2(х-8)
(х+5)6х2
· Преобразуем:
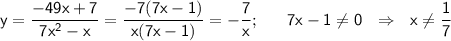
Функция разрывна в точках x = 0 (бесконечный разрыв), x = 1/7 (выколотая точка).
· Графиком функции является гипербола. Таблица точек для построения:
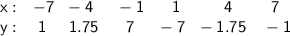
Готовый график смотреть на первой картинке.
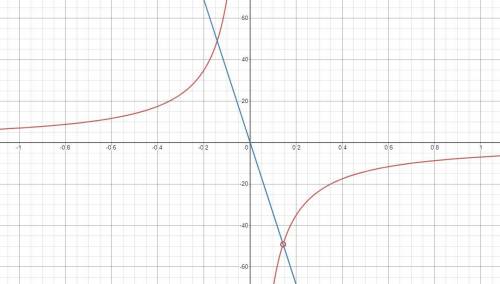
· Прямая y = kx есть прямая, проходящая через начало координат. Коэффициент k задает ее угол наклона. Чтобы прямая пересекла график только в одной точке, пустим ее через найденную ранее выколотую точку (см. вторую картинку).
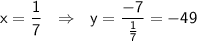
- это координаты выколотой точки. Подставим в уравнение:
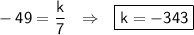
Других случаев с одним пересечением нет: при k ∈ [0, +∞) пересечения отсутствуют, при k ∈ (-∞, -343) ∪ (-343, 0) пересечения два.
ответ: k = -343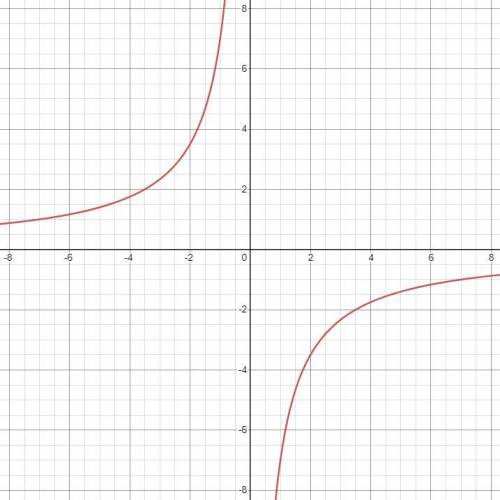
а) E(y) = [-4; +∞)
б) x ∈ (-∞; 0) ∪ (4; +∞)
в) x ∈ (2; +∞)
Объяснение:
у = (х - 2)²- 4
Це парабола, вітви якої направлені догори. За рівнянням вершина знаходиться у точці: (2; -4).
а) область значення функції:
E(y) = [-4; +∞) - визначили за графіком (на фото).
б) проміжки, на яких функція набуває додаткових значень:
За графіком бачимо, що y > 0 на двох інтервалах:
(-∞; 0) ∪ (4; +∞)
б) проміжок зростання функції:
Це парабола, тому на першому проміжку: x ∈ (-∞; 2) функція спадає, а на проміжку: x ∈ (2; +∞) зростає.

(c-2)(c+3)-c^2=c^2+3c-2c-6-c^2=c-6
7(х+8)+(х+8)(х-8)=7x+56+x^2-8x+8x-64=x^2+7x-8
(х+5)4х-(2х+5)^2=4x^2+20x-4x^2+20x+25=40x+25