y=x²-2x+3
А) хо= -b/2a = -(-2)/2 = 2/2 =1
yo= f(xo) = 1²-2*1+3 = 1-2+3= 2
(1; 2)
Б) Ось симиетрии параболы -- это, по сути, просто приравнивание игрека к хо: у=1
В) С осью Ох:
На оси Ох ордината равна нулю, поэтому просто заменяем игрек на ноль и решаем
x²-2x+3=0
D= (-2)²-4*3 = 4-12= -8
D<0
График не имеет точки пересечения с осью Ох ∅.
С осью Оу:
На оси ординат значение абсциссы (х) равно нулю. Поэтому подставляем вместо икса ноль:
y=0²-2*0+3
y=3
Поэтому точка пересечения данного графика с осью Оу -- (0; 3)
Г) на фото. Направление веток параболы--вверх, потому что а>0
Еще мы там уточняем график
Д) в первой и во второй
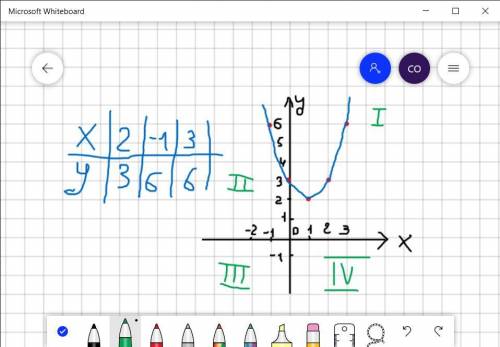
Вообще область значений тангенса и котангенса - все действительные числа:
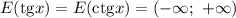
а)
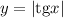
Если рассмотреть модуль тангенса, то отрицательные значения примут противоположные значения, то есть станут положительными. Нулевое и положительные значения сохранятся. Получим область значений:
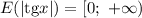
б)
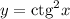
Котангенс может принять значение любого действительного числа, но при возведении любого числа в квадрат результат получится неотрицательным.
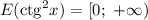
в)
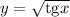
Тангенс может принять значение любого действительного числа. Под знак корня из них можно записать любое неотрицательное, при этом в результате может получиться любое неотрицательное число.
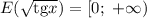
г)
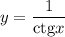
Котангенс может принять значение любого действительного числа. При делении 1 на любое число (отличное от нуля) может получиться любое число, кроме нуля.
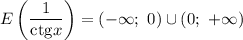
что могла, то решила) Надеюсь, что это
Объяснение: