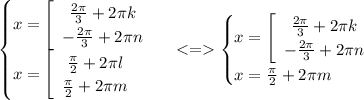
(1)РЕШЕНИЕ:![sin(2x)+sin(x)=2cos(x)+1; \ [\pi;3\pi]\\ sin(x)\cdot (2cos(x)+1)=2cos(x)+1;\\ (2cos(x)+1) \cdot (sin(x)-1) = 0;\\ \begin{cases} cos(x)=-\frac{1}{2}\\sin(x)=1 \end{cases}\\ \begin{cases} x=\left[\begin{array}{ccc}arccos(-\frac{1}{2})+2\pi k \\ -arccos(-\frac{1}{2}) +2\pi n \end{array}\right\\x=\left[\begin{array}{ccc}arcsin(1)+2\pi l\\ \pi - arcsin(1)+2\pi m\end{array}\right\end{cases}\\](/tpl/images/0166/9322/f5b34.png)
(2)ВЫБОРКА: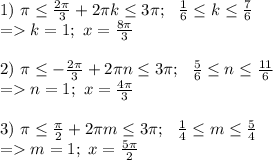
(3)ОТВЕТ: 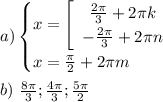
Объяснение:
1) Приводишь к общему знаменателю и при этом выполняется:
6х - 1 ≠ 0
х ≠ 1/6
(x+2)(6x-1) = 15
6x^2-x+12x-2-15 = 0
6x^2+11x-17 = 0
D = b^2-4ac
D = 11^2-4*6*(-17) = 121+408 = 529
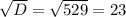
x1 = (-b+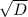 )/2a = (-11+23)/2*6 = 12/12 = 1
)/2a = (-11+23)/2*6 = 12/12 = 1
x2 = (-b-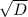 )/2a = (-11-23)/2*6 = -34/12 = -17/6
)/2a = (-11-23)/2*6 = -34/12 = -17/6
ответ: 1; -17/6
2) Чтобы найти точку пересечения двух графиков достаточно их приравнять и решить уравнение, т.е.:
2/x = x-1
2/x - x + 1 = 0
-x^2+x+2 = 0 Домножим на (-1):
x^2 -x -2 =0
по т. Виета:
x1+x2 = 1
x1*x2 = -2
x1= 2 x2= -1
Если x = 2, то у = 1
Если х = -1, то у = -2
ответ: (2;1) и (-1;-2)