Определим общее число расстановок на пяти позициях 5 шариков:
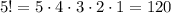
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах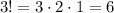 
Таким образом, всего имеется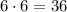 
недопустимых расстановок.
Значит, допустимых расстановок имеется:
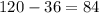
ответ: 84
Объяснение:
Опишем общую схему решения задач с систем уравнений:
1. Для неизвестных величин вводим определенные обозначения и составляем систему линейных уравнений.
2. Решаем полученную систему линейных уравнений.
3. Использую введенные обозначения, записываем ответ.
Попробуем применить данную схему на конкретной задаче.
Известно что, два карандаша и три тетради стоят 35 рублей, а две тетради и три карандаша стоят 40 рублей. Необходимо выяснить, сколько стоят пять карандашей и шесть тетрадей.
Нам необходимо найти, сколько стоит по отдельности один карандаш и одна тетрадь. Если такие данные у нас будут, то решить, сколько стоят пять карандашей и шесть тетрадей, не составит труда.
Обозначим за х цену одного карандаша в рублях. А у - цена одной тетради в рублях. Теперь внимательно читаем условие и составляем уравнение.
«два карандаша и три тетради стоят 35 рублей» значит
2*x+3*y = 35;
«две тетради и три карандаша стоят 40 рублей» следовательно
3*x+2*y = 40;
Получаем систему уравнений:
{2*x+3*y = 35;
{3*x+2*y = 40;
С первым пунктом покончено. Теперь необходимо решить полученную систему уравнений любым из известных
Решив, получаем х=10, а y=5.
Вернувшись к исходным обозначениям имеем, цена одного карандаша 10 рублей, а цена одной тетрадки 5 рублей.
Осталось посчитать, сколько стоят пять карандашей и шесть тетрадок. 5*10+6*5=80.
ответ: 80 рублей.