Решаем методом замены.
Пусть x² + 4x = a, тогда получаем уравнение
a(a - 17) = -60
a² - 17a = -60
a² - 17a + 60 = 0
По теореме Виета находим корни:
a1 = 5; a2 = 12
Возвращаемся к старым переменным, учитывая, что a = x² + 4x:
x² + 4x = 5 или x² + 4x = 12
x² + 4x - 5 = 0 x1 = -6;x2 = 2
x1 = -5;x2 = 1
Таким образом, данное уравнение имеет 4 корня:
-6; -5; 1; 2
Сделаем замену сначала: 7x=t, т.е 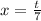
Поскольку x->0, то и 7x->0, значит и t->0.
Подставляем в наш предел то что получилось с учетом замены:
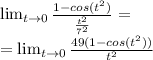
Поскольку нас неопределенность 0/0 можно использовать правило Лопиталя.
Получаем:
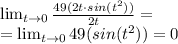
Возможно я не так понял задание и там имелось в виду:
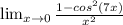
Тогда используем ту же самую замену.:
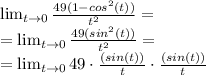
Видим что здесь произведение двух "первых замечательных пределов", а именно:
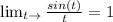
Используем этот факт и получим: 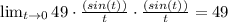
Как-то так. Но обязательно проверь.
поскольку многочлен состоит из одночленов, то суть метода состоит в том, чтобы найти в каждом одночлене в составе многочлена, такой множитель, чтобы он присутствовал в каждом одночлене(берём по возможности низшую степень множителя). Сейчас объясню на практике, а то на словах трудновато:
в данном многочлене надо в каждом одночлене найти общий делитель, на который одновременно делятся и первый и второй одночлен. Исследуем этот многочлен.
Проверю сначала числовые множители, входящие в каждый одночлен. Замечаю, что 2 является частью общего множителя. поскольку 2 делится на 2, а 6 также делится на 2.Значит, записываю начало разложения: 2
Далее, проверю переменную x. Она есть в каждом одночлене, только во втором одночлене она в квадрате. Следовательно, надо записать в разложение также x(она содержится в обоих одночленах), но выбрать в разложение низшую степень x, то есть в разложение мы запишем x, а не x². Это будет вторая часть общего множителя. Он имеет теперь вид 2x. Проверим, есть ли ещё часть общего мнодителя. Я вижу, что переменная y содержится только в одном одночлене, а в другом его нет. Значит, он не является частью общего множителя. больше ничего в одночленах нет. Значит, общий множитель здесь будет 2x.
Теперь разделим каждый член многочлена на 2x. В первом одночлене 2 делим на 2, остаётся 1, x делим на x, остаётся 1. остался нетронутым только y. Поэтому первый одночлен будет иметь вид y. Во втором одночлене поделим 6 на 2, будет 3. x² делим на x(мы делим соответственно число на число, букву на букву), получаем x. Теперь преобразованный вариант пишем в скобках. итог:
2x(y-3x). То есть суть метода заключается в том, что мы по приведённым правилам, ищем общий для всего многочлена делитель, а затем почленно делим его на этот множитель.Выявленный общий множитель выносим за скобки, а поделённый многочлен - в скобках. Мы разложили данный многочлекн на множители )