1) p=1, q-любое; p=-2, q=-1.
2) 1728x²-224x+1=0
Объяснение:
2.75.1)
Если u, v - корни уравнения x²+px+q=0, то u+v=-p, uv=q.
Если u+1, v+1 - корни уравнения x²-p²x+pq=0, то (u+1)+(v+1)=p², (u+1)(v+1)=pq.
Получились уравнения:
u+v=-p,
uv=q,
(u+1)+(v+1)=p²,
(u+1)(v+1)=pq.
Выпишем третье уравнение: (u+v)+2=p². Подставим туда первое уравнение: -p+2=p². Отсюда p²+p-2=0, откуда p=1 или p=-2.
Рассмотрим 4 уравнение: uv+(u+v)+1=pq. Подставим туда 1 и 2 уравнения: q-p+1=pq, откуда (p-1)(q+1)=0. То есть p=1 или q=-1.
Получим систему из совокупностей уравнений.
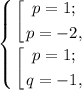
Если p=1, то q - любое значение
Если q=-1, то p=1 или p=-2
Окончательный ответ: p=1, q-любое; p=-2, q=-1.
2.75.2)
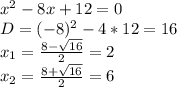
Новые корни уравнения: 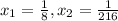
Искомое квадратное уравнение:
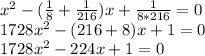
1)1,3; 2,1;...;
Дано:
a1 =1,3;
a2 = 2,1;
Найти:
а20 и S20
Для начала найдем разность-d
для этого от 2-го члена вычтем 1-ый:
d= 2,1 - 1,3= 0,8;
по формуле :an= a1-(n-1)×d найдем "а20"
а20=а1+(20-1)×d=a1+19d
Подставим готовые значения:
a1+19d= 1,3+19×0,8=16,5;
а20=16,5.
Теперь узнаем S20:
по формуле:
а1+аn/2 ×n (я использую самою простую формулу ,но вторая тоже подойдёт только с ней решать дольше)
S20= 1,3+a20/2 ×20={сократить 2 и 20}далее запись:
(1,3+а20)×10=(1,3+16,5)×10=178;
ответ: а20=16,5; S20=178.
P.s: аn -20-ый член.
Sn- сумма 20 первых членов прогрессии.
1)6
-
9
2) там что
3)6x
дробь
Объяснение:
1)8x+x=6
9x=6
x=6
_
9
2)не полностью написали
3)7x=x
7x-x=0
6x=0