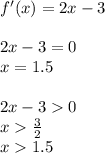
Объяснение:
f(x)=x²-3x+1
f'(x)=(x²-3x+1)' = (x²)' + (-3x)' + (1)' =
= 2x -3 + 0 = 2x-3
f'(x)=0 → 2x-3=02x=0+3
2x=3
x=3/2
x=1,5
f'(x)>0 → 2x-3>02x>0+3
2x>3
x>3/2
x>1,5
1. u = 7-2v
(7-2v)^2 + 4v - 13 =0
49 - 28v + 4v^2 + 4v - 13 = 0
4v^2 - 24v + 36 = 0 (:4)
v^2 - 6v + 9 = 0
(v - 3)^2 = 0
v =3
u = 7 - 2*3 = 7-6=1
ответ : v=3, u=1
2. z = -3+y^2
y^2 + 3*(y^2-3)-7=0
y^2 +3y^2 - 9-7 = 0
4y^2 - 16 = 0
4*(y^2-4)=0
y = 2 y=-2
z = 4-3=1 z = 4-3=0
ответ : y = 2, z=1; y=-2, z=1
3. m = 7+2n
(7+2n)^2 +5n + 14 = 0
49 + 28n + 4n^2 + 5n + 14 = 0
4n^2 + 33n + 65 = 0
D = 1089 - 1040 = 49
n1 = -33+7/8 = -26/8 = -3,25
n2= -33-7/8 = -40/8 = -5
m1 = 7 - 2 * 26/8 = 7-6,5 = 0,5
m2 = 7 - 2*5 = 7-10 = -3
ответ : n=-3,25,m=0,5 ; n=-5, m=-3
4. 2k = 7+2t^2
k = 7+2t^2/2
3*(7+2t^2/2) + 5t - 20 = 0
6t^2 + 10t - 19 = 0
D = 784
t1 = 1,5
t2 = -19/6
k1 = 5,75
k2 = 13 19/36