Обе функции монотонно возрастающие.
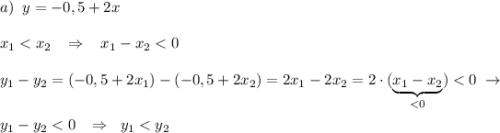
Получили, что мЕньшему значению переменной соответствует мЕньшее значение функции, и наоборот, бОльшему значению переменной соответствует бОльшее значение функции. Значит функция возрастающая .
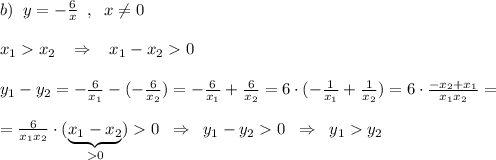
Знак выражения получили (+) , так как произведение 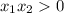 в силу того, что гиперболу рассматриваем на двух промежутках при
в силу того, что гиперболу рассматриваем на двух промежутках при 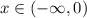 и при
и при 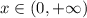 , где
, где 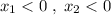 и
и 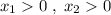 .
.
Получили, что бОльшему значению переменной соответствует бОльшему значение функции, и наоборот, мЕньшему значению переменной соответствует мЕньшему значение функции. Значит функция возрастающая .
В решении.
Объяснение:
Задание на разность квадратов: а² - в² = (а - в)*(а + в).
1)(х-2)²-4 = (х - 2 - 2)*(х - 2 + 2) = х(х - 4);
2) (b+7)²-100c² = (b + 7 - 10c)*(b + 7 + 10c);
3) 121-(b+7)² = (11 - b - 7)*(11 + b + 7) = (4 - b)*(b + 18);
4) a⁴-(7b-a²)² = (a² - 7b + a²)*(a² + 7b - a²) = 7b*(2a² - 7b);
5) (4x-9)²-(2x+19)² = (4x - 9 - 2x - 19)*(4x - 9 + 2x + 19) = (2x - 28)*(6x + 10);
6) (a+b+c)²-(a-b-c)² = (a + b + c - a + b + c)*(a + b + c + a - b - c)=2a*(2b+2c).