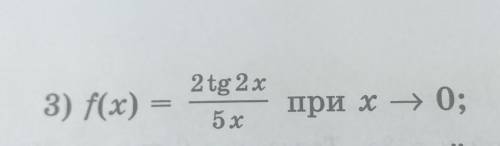
Первую ещё не придумала, а вот вторая:
Чтобы найти вероятность того, что точка,брошенная в круг, попадёт в треугольник, надо найти отношение площади правильного треугольника к площади окружности
S(треуг)=(а:2*корень(3))/ S 4
S(окруж)=Pі *r^2
Мы знаем связь между стороной правильного треугольника и радиусом описаной окружности:
r=a/корень3
Тогда, вероятность = S(треуг)/ S(окруж)= ((а:2*корень(3))/ S 4) / (Pі *r^2) = ((а:2*корень(3))/ S 4) * (Pі *а^2) /3=(3*корень3)/ 4Pі
Если надо, можно примерно вищитать:
(3*корень3)/ 4Pі = 3*1,73/4*3,14=5,19/12,56=0,41
ответ:0,41
Объяснение:
ОДЗ : cos2x ; sin2x
cosx ± 1/4 ; sinx ; cosx 0
x ± arccos0,25 + 2πk ; x πk/2 , k ∈ z
2*2cos^2 x - 2 = 1/2cos2x * ( ... )
2cos2x = 1/2cos2x * ( ... )
можно поделить на cos2x, так как cos2x также есть в знаменателе, то есть корни мы не теряем
2 = 1/2 * ( ... )
для удобства делаем замену: пусть 2x = t
2 = 1/2 * (/cost + 1/sint)
2 = /2cost + 1/2sint
(sint + cost) / 2costsint = 2
-2 (-/2 sint - 1/2 cost) / 2costsint = 2
-2 (-sin (π/3) sint - cos(π/3) cost) / 2costsint = 2
выносим минус за скобки и сокращаем 2
а также, используя формула приведения косинуса, только в обратную сторону, делаем все красиво
cos (π/3 - t) / costsint = 2
cos (π/3 - t) = 2costsint
cos (π/3 - t) - sin2t = 0
sin (π/2 - (π/3 - t) - sin2t = 0
sin (π/6 + t) - sin2t = 0
используем sin(t) - sin(s) = 2cos((t + s)/2) * sin ((t - s)/2)
и делим на 2
cos ((π + 18t)/12) * sin((π - 6t)/12) = 0
cos ((π + 18t)/12) = 0
sin ((π - 6t)/12) = 0
t = 5π/18 + 2πk/3
t = π/6 + 2πk
вспоминаем, что t = 2x
x = 5π/36 + πk/3
x = π/12 + πk
k ∈ Z
4/5
Объяснение:
для решения данного примера необходимо знать одно из следствий первого замечательного предела:
lim (x→0) (tg x)/x = 1
3) lim (x→0) (2 tg 2x)/5x =
(используя следствие первого замечательного предела):
=lim (x→0) (2 * 2 tg 2x)/(5х*2)=
=lim (x→0) (2*2/5)* ( tg 2x)/2x =
= (2*2/5) * lim (x→0) ( tg 2x)/2x =
[ х→0, соответственно 2х→0]
= (2*2/5) * lim (2х→0) ( tg 2x)/2x =
= (2*2/5) * 1 = 4/5 * 1 = 4/5
( используя правило Лопиталя):
= lim (x→0) (2 tg 2x)' / (5x)' =
= lim (x→0) (2 * (2х)' * (1 / cos² 2x)) / 5 =
= lim (x→0) (2*2 / cos² 2x) / 5 =
= lim (x→0) (2*2/5) * ( 1/ cos² 2x) =
= (2*2/5) * lim (x→0) (1/cos²(2x)) =
= 4/5 * (1/cos²(2*0))=
= 4/5 * 1/1² = 4/5 * 1 = 4/5