
18 (км/час) - собственная скорость лодки
6 (км/час) - скорость течения реки
Объяснение:
Моторная лодка в первый день км по течению реки за 5ч, а во второй день она км против течения за 6ч. Найти собственную скорость лодки и скорость течения реки
х - собственная скорость лодки
у - скорость течения реки
х+у - скорость лодки по течению
х-у - скорость лодки против течения
Согласно условию задачи составляем систему уравнений:
120/(х+у)=5
72/(х-у)=6
Умножим первое уравнение на (х+у), второе на (х-у), избавимся от дроби:
120=5(х+у)
72=6(х-у)
5(х+у)=120
6(х-у)=72
5х+5у=120
6х-6у=72
Разделим первое уравнение на 5, второе на 6 для удобства вычислений:
х+у=24
х-у=12
Выразим х через у в первом уравнении, подставим выражение во второе уравнение и вычислим у:
х=24-у
24-у-у=12
-2у=12-24
-2у= -12
у= -12/-2
у=6 (км/час) - скорость течения реки
х=24-у
х=24-6
х=18 (км/час) - собственная скорость лодки
Проверка:
120:24=5 (часов) по течению
72:12=6 (часов) против течения, всё верно.
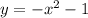
а < 0 ⇒ ветви направлены вниз
-х²-1 ⇒ график функции сдвигается вниз по оси ординат на 1
Подходящий график: Б
2.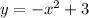
а < 0 ⇒ ветви направлены вниз
-х²+3 ⇒ график функции сдвигается вверх по оси ординат на 3
Подходящий график: Г
3.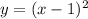
а > 0 ⇒ ветви направлены вверх
(х-1)² ⇒ график функции сдвигается вправо по оси абсцисс на 1
Подходящий график: Д
4.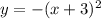
а < 0 ⇒ ветви направлены вниз
(x+3)² ⇒ график функции сдвигается влево по оси абсцисс на 3
Подходящий график: А
5.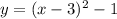
а > 0 ⇒ ветви направлены вверх
(x-3)²-1 ⇒ график функции сдвигается вправо по оси абсцисс на 3, да ещё вниз по оси ординат на 1
Подходящий график: Е
6.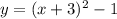
а > 0 ⇒ ветви направлены вверх
(x+3)²-1 ⇒ график функции сдвигается влево по оси абсцисс на 3, да ещё вниз по оси ординат на 1
Подходящий график: В
x³ - y³
Объяснение:
Формула: (a-b)(a²+ab+b²)= a³-b³
То есть (x-y)(x²+xy+y²) = x³-y³