
1) Найди дискриминант квадратного уравнения 8x²+4x+12=0.
D = b² - 4ac = 16 - 4·8·12 = 16 - 384 = -368.
2) Найди корни квадратного уравнения x²+7x+12=0.
По т., обратной к т. Виетта, имеем х₁ = -4; x₂ = -3.
3) Реши квадратное уравнение 2(5x−15)²−7(5x−15)+6=0.
Рациональным будет метод введения новой переменной.
Пусть 5x−15 = t, тогда имеем:
2t²−7t+6=0; D = b² - 4ac = 49 - 4·2·6 = 49 - 48 = 1; √D = 1
t₁ = (7 + 1)/4 = 2; t₂ = (7 - 1)/4 = 1,5.
Возвращаемся к замене:
5x−15 =2; 5x = 2 + 15; 5x = 17; x = 17/5; x₁ = 3,4.
5x−15 = 1,5; 5x = 1,5 + 15; 5x = 16,5; x = 16,5/5; x₂ = 3,3.
ответ: 3,4; 3,3.
4)Найди корни уравнения −8,9(x−2,1)(x−31)=0.
x−2,1 = 0 или x−31 = 0.
х₁ = 2,1 х₂ = 31.
ответ: 2,1; 31.
5) Сократи дробь (x−4)²/(x²+2x−24) = (x−4)²/((x + 6)(x − 4)) = (х - 4)/(х + 6).
Полученная дробь: (х - 4)/(х + 6).
6)Сократи дробь (5x²−32x+12)/(x³−216).
5x²−32x+12 = 0; D = b² - 4ac = 1024 - 480 = 784; √D = 28.
x₁ = (32 + 28)/10 = 6; x₂ = (32 - 28)/10 = 0,4
Имеем: (5x²−32x+12)/(x³−216) = ((x - 6)(5x - 2))/((x - 6)(x² + 6x + 36)) =
= (5x - 2)/(x² + 6x + 36).
7) Разложи на множители квадратный трехчлен x² + 8x + 15.
x² + 8x + 15 = 0; x₁ = -3; x₂ = -5.
имеем, x² + 8x + 15 = (x + 3)(x + 5).
1) 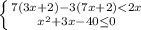
7(3x+2)-3(7x+2)<2x
21x+14-21x-6<2x
8<2x
-2x<-8
x>4
x²+3x-40≤0
x²+3x-40=(x-5)(x+8)
D=13²
x1=5
x2=-8
(x-5)(x+8)≤0
5 -8
x∈[-8;5]
После объединения в один чертёж:
ответ: x∈(4;5]
2) 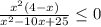
x²-10x+25≠0
D=0
x≠5
x²-10x+25=(x-5)²
x²(4-x)≤0
-x²(x-4)≤0
⇒ -x²(x-4)*(x-5)²≤0
-x²=0
x=0(знак на чертеже дублируется)
x-4=0
x=4
(x-5)²=0
x=5(знак дублируется и 5 выкалывается)
ответ: x∈[4;5)∪(5;∞)
3) 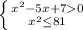
x²-5x+7>0
x²-5x+7
D=25-28=-3
⇒x>0 при любых x
Дополнительно: После D=-x - не всегда неравенство имеет решение - надо смотреть по графику (в вашем случаи - при любых x)
x²≤81
x²-81≤0
(x-9)(x+9)≤0
9;-9
ответ: x∈[-9;9]
вот вам решение, правильно тут