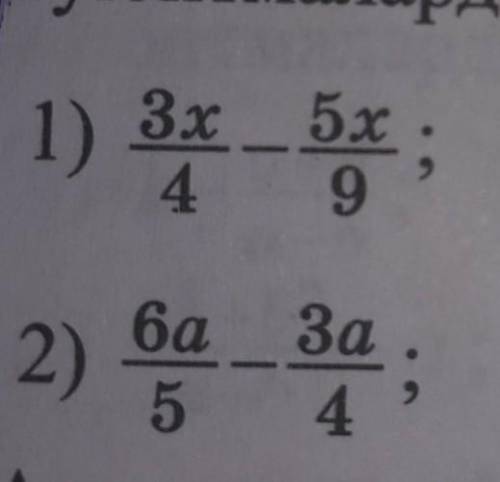
Нарисуем график функции Y = √ X как повернутую на 90 градусов левую половину параболы Y = X².
1) Проведем горизонтальную прямую Y = 3. Она пересекает данный график при Х = 9
2) Проведем горизонтальную прямую Y = 5. Она пересекает данный график при Х= 25
3) Проведем прямую Y = X (биссектрису прямого угла). Она пересекает график при Х = 0 и Х = 1. Следовательно, уравнение имеет 2 корня.
4) Поскольку функция корня определена при Х ≥ 0, то -Х ≤ 0 и, следовательно решением может быть только Х = 0. Это значение и будет единственным корнем.
чертишь график для первого
дискриминант равен минус б в квадрате минус 4ас это получается 1+24=25 находим корни минус б плюс(для первого) минус(для второго) дискриминант и все это деленное на 2а х1=3 а х2=-2
для второго
х=1 значит у=3 х=0 значит у=2
чертим графики первый порабола вветви вверх второй прямая
смотрим что график прямая проходит выше параболы значит будем из 2й функции вычитать 1ую
найдем предел интеграла
х^2-x-6-x-2=0
x^2-2x-8=0
d=36
x1 = 4
x2 = -2
интеграл -2 4 (x+2) - (x^2 -x-6) = интеграл -2 4 ( x + 2 - x^2 + x + 6) = интергал -2 4 (-x^2 +2x + 8) = x^3/3 + x^2 + 8x = затем подставляем в урравнение -2 и 4 и получаем ответ
3x/4 -5x/9=3x*9-5x*4 /36=27x-20x/36=7x/36
6a/5 -3a/4=6a*4-3a*5/20=24a-15a/20=9a/20