Такой формулы - нет
Объяснение:
Такой формулы нет. Основные формулы, это:
(a+b)^2 = a^2+2ab+b^2 – квадрат суммы
(a-b)^2 = a^2-2ab+b^2 – квадрат разности
a^2-b^2 = (a-b)(a+b) – разность квадратов
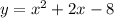
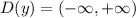
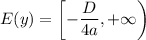 - где D дискриминант.
- где D дискриминант.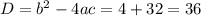
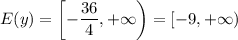
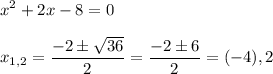
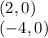



![(-\infty,-1]](/tpl/images/0467/5865/91666.png)
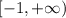

Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)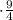 - объем работы системы из двух насосов за 2ч 15мин.
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: 
9t = 1

Значит, 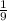 - цис./ч - производительность "медленного" насоса.
- цис./ч - производительность "медленного" насоса.
Тогда 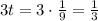 - цис./ч - производительность "быстрого" насоса.
- цис./ч - производительность "быстрого" насоса.
Следовательно, 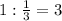 ч - потребуется "быстрому" насосу на заполнение цистерны.
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.

Формулы для квадратов
(a + b)2 = a2 + 2ab + b2 – квадрат суммы
(a – b)2 = a2 – 2ab + b2 – квадрат разности
a2 – b2 = (a – b)(a + b) – разность квадратов
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
Формулы для кубов
(a + b)3 = a3 + 3a2b + 3ab2 + b3 – куб суммы
(a – b)3 = a3 – 3a2b + 3ab2 – b3 – куб разности
a3 + b3 = (a + b)(a2 – ab + b2) – сумма кубов
a3 – b3 = (a – b)(a2 + ab + b2) – разность кубов
Формулы для четвёртой степени
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
(a – b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4
a4 – b4 = (a – b)(a + b)(a2 + b2)
Формулы для n-той степени
(a + b)n = an + nan – 1b + n(n – 1) 2 an – 2b2 + ... + n! k!(n – k)! an – kbk + ... + bn
(a - b)n = an - nan – 1b + n(n – 1) 2 an – 2b2 + ... + (-1)k n! k!(n – k)! an – kbk + ... + (-1)nbn
Объяснение:
Надеюсь все понятно