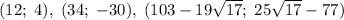
Объяснение:
![\sqrt{x+y}+\sqrt[3]{x-y}=6\\\sqrt[6]{(x+y)^3(x-y)^2}=8](/tpl/images/1358/0734/79d4c.png)
Выполним преобразование:
![\sqrt{x+y}+\sqrt[3]{x-y}=6\\\sqrt{x+y}\times\sqrt[3]{x-y}=8](/tpl/images/1358/0734/48821.png)
или ![\sqrt{x+y}+\sqrt[3]{x-y}=6\\\sqrt{x+y}\times\sqrt[3]{x-y}=-8](/tpl/images/1358/0734/9c2ec.png)
Пусть ![\sqrt{x+y}=k,\;\sqrt[3]{x-y}=t](/tpl/images/1358/0734/e7517.png)
.
Тогда для 1-ого случая:
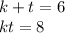
Заметим здесь теорему Виета (если не заметили, то можно просто решить эту систему).
Тогда:
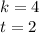
или
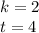
Замечу, что замену можно было не делать. Она дана для понимания. Можно было сразу написать то, что идет после слов обратная замена.
Обратная замена:
![1)\\\sqrt{x+y}=4\\\sqrt[3]{x-y}=2](/tpl/images/1358/0734/fbf65.png)
Первое уравнение можно возвести в квадрат, так как обе части его положительны:
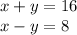
Очевиден прием решения: сложение.
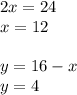
Получили пару чисел (12; 4).
![2)\\\sqrt{x+y}=2\\\sqrt[3]{x-y}=4\\\\x+y=4\\x-y=64\\\\2x=68\\x=34\\\\y=4-x\\y=-30](/tpl/images/1358/0734/7b359.png)
Получили пару (34; -30).
Для 2-ого случая:
![\sqrt{x+y}+\sqrt[3]{x-y}=6\\\sqrt{x+y}\times\sqrt[3]{x-y}=-8\\\\\sqrt{x+y}=3+\sqrt{17}\\\sqrt[3]{x-y}=3-\sqrt{17}\\\\x+y=(3+\sqrt{17})^2\\x-y=(3-\sqrt{17})^3\\\\x=103-19\sqrt{17}\\y=25\sqrt{17}-77](/tpl/images/1358/0734/218c4.png)
Еще одна пара чисел: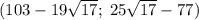 
Заметим, что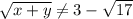 
, т.к. это число меньше 0.
Система уравнений решена!
Объяснение:
Чтобы выяснить проходит ли данная функция через эти точки надо :
1) либо построить график функции на координатной плоскости, потом отметить эти точки и посмотреть, лежать ли они на этом графике.
: более легкий: просто подставить координаты точек В и С в уравнение графика функции y=-1/5x
У точки В координаты (-15;3), значит х=-15, у=3
Подставляем в уравнение у=-1/5х
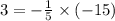
Если справа перемножить, то будет 3, ответы совпадают 3=3
Значит график функции проходит через точку В.
Аналогичным образом поступим с точкой С:
С(1;-5). Х=1, у=-5
Подставляем и проверяем :
-5=-1/5*1
-5=-1/5 неверно
Значит данный график функции не проходит через точку С
4^x≤9-2^x +22
2^2x≤9-2^x +22
2^x=a a>0
a^2≤9-a+22
a^2+a-31≤0
В этом варианте корень нецелый. Предполагаю ошибку в примере. В любом случае - решается тем-же что и слелующий.
4^x≤9*2^x +22
2^2x≤9*2^x +22
2^x=a a>0
a^2-9a-22≤0
(a-11)(a+2)≤0
Итого: -2≤a≤11, не забываем область определения a>0.
Получаем: 0<a≤11
lg(3)[x^2-x-2]≤1+lg(3)[(x+1)(x-2)]
(x+1)(x-2)>0
x<-1; x>2
g(3)[(x-2)(x+1)]-lg(3)[(x+1)(x-2)]≤1
lg(3)[((x+1)(x-2))/((x-2)(x+1))]≤1
lg(3)[1]≤1
Выражение истинно всегда. Значит ограничение только в области определения.
ответ: x<-1; x>2