Если первая труба наполняет бассейн за х часов, то вторая за (х+8) часов, в час первая труба наливает 1/х бассейна, вторая 1/(х+8) часть бассейна, за 3 часа вместе они наливают целый бассейн:
3*(1/х+1/(х+8)) = 1
общий знаменатель х*(х+8)
числитель будет: 3*(х+8+х)
дробь равна 1, значит числитель равен знаменателю
3*(2х+8) = х^2+8х
х^2+8x-6x-24 = 0
x^2+2x-24=0
D=4+96 = 100
x=(-2+-10)/2
x=-6 или х=4
Отриц. значение не подходит по смыслу задачи, значит х=4
в задаче спрашивалось про 2 трубу, она наполнит бассейн за 4+8 = 12 часов
a)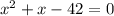 
Ищем дискриминант:
D=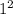
-4*1*(-42)=1-4*(-42)=1-(-4*42)=1-(-168)=1+168=169;
Дискриминант больше 0, уравнение имеет 2 корня: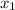
=
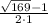=(13-1)/2=12/2=6;
= 
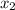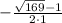=(13-1)/2=12/2=6 =(-13-1)/2=-14/2=-7.
б)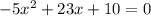 
Ищем дискриминант:
D=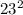
-4*(-5)*10=529-4*(-5)*10=529-(-4*5)*10=529-(-20)*10=529-(-20*10)=529-(-200)=529+200=729;
Дискриминант больше 0, уравнение имеет 2 корня: =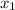 
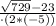=(27-23)/(2*(-5))=4/(2*(-5))=4/(-2*5)=4/(-10)=-4/10=-0.4;
= 
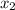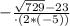=-50/(2*(-5))=-50/(-2*5)=-50/(-10)=-(-50/10)=-(-5)=5.
в)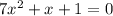 
Ищем дискриминант:
D=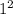-4*7*1=1-4*7=1-28=-27;
Дискриминант меньше 0, уравнение не имеет корней.
г)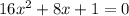 
Ищем дискриминант:
D=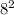 
-4*16*1=64-4*16=64-64=0;
Дискриминант равен 0, уравнение имеет 1 корень:
X=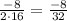
=-0.25
Объяснение:
1) 3x-6
2) 6m+18n
3) 64-c²
4) 8a³+125b³