В решении.
Объяснение:
Нужно изучить свойства корней.
а) (2√5 + 3√2)(√5 - √8)=
=(2√5 + 3√2)(√5 - √4*2)=
=(2√5 + 3√2)(√5 - 2√2)=
умножить каждый член первых скобок на каждый член вторых скобок:
=2√5 * √5 + 3√2 * √5 - 2√5 * 2√2 - 3√2 * 2√2 =
= 2 * 5 + 3√10 - 4√10 -6 * 2 =
=10 - 12 - √10 =
= -2 - √10;
б) (√11 - 0,5√22)(0,5√22 + √11) =
умножить каждый член первых скобок на каждый член вторых скобок:
=√11*0,5√22 + √11*√11 - 0,5√22*0,5√22 - 0,5√22*√11 =
=0,5√242 + 11 - 0,5*22 - 0,5√242 =
=0,5√242 + 11 - 11 - 0,5√242 =
=0 (все члены выражения взаимно уничтожаются).
в) (√42)² - (2√6 - 3√2)²=
вторые скобки квадрат разности, по формуле сокращённого умножения:
=42 - [(2√6)² - 2*2√6*3√2 + (3√2)²]=
=42 - (4*6 -12√12 + 9*2)=
=42 - (24 - 12√4*3 + 18)=
=42 - (24 - 12*2√3 + 18)=
=42 - (42 - 24√3)=
=42 - 42 + 24√3=
=24√3.
Вертикальные асимптоты: x = 2
Горизонтальные асимптоты: y = 3
Нет наклонных асимптот
Объяснение:
Выясним, при каких значениях переменной функция 3 x + 1 x − 2 не определена. x = 2
Рассмотрим рациональную функцию
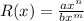, где n - степень числителя, а m - степень знаменателя.
1. Если n < m , то ось x, y = 0 , является горизонтальной асимптотой.
2. Если n = m , то горизонтальной асимптотой является прямая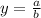 
Если n > m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем n и m
n = 1 ; m = 1
Поскольку n = m , горизонтальная асимптота является прямой 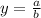, где a = 3 и b = 1
y = 3
Наклонных асимптот нет, поскольку степень числителя меньше либо равна степени знаменателя.
Это множество всех асимптот.
Вертикальные асимптоты: x = 2
Горизонтальные асимптоты: y = 3
Нет наклонных асимптот
а) y=sin(x/2)
y=f(п/2)+f'(п/2)(x-п/2)
f(п/2)=sin(п/4) = √2/2
f'(x)=1/2*cos(x/2)
f'(п/2)= 1/2*cos(п/4)=1/2 * √2/2= √2/4
y=√2/2 + √2/4*(x-п/2)
y=√2/2+x√2/4 - п√2/8
y=x√2/4 + √2/2 - п√2/8
б) y=x^2-2x
y=f(2)+f'(2)(x-2)
f(2)=4-4=0
f'(x)=2x-2
f'(2)=4-2=2
y=0+2(x-2)
y=2x-4