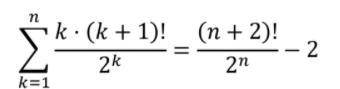
нет
Объяснение:
1) 20 000 000 *5= 100 000 000 л воды будет разлито по 5 литровым бутылкам за 1 год
2) 100 000 000 *3= 300 000 000 л воды будет разлито за 3 года
3) Площадь озера 31 722 км² , а объем воды 300 000 000 л
переведем км² в м² , а л в м³
1 м³ = 1000 л
1 км²= 1000000 м², значит
31 722 км²= 31722 * 1000000= 31 722 000 000 м²
300 000 000 л = 300 000 000 : 1000=300 000 м³
Найдем насколько понизится уровень воды :
300 000 м³ : 31 722 000 000 м²= 3 : 317220 ≈0,0000095 м или
1 м = 1000 мм
0,0000095 * 1000 = 0,0095 мм
Как видим уровень понижения воды не составит даже 1 мм ,значит понижение воды , вызванное деятельностью завода , не будет заметно.
Объяснение:
1) (x-6)*(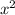 +6x+36)=
+6x+36)=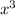 -
-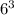 =
=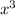 -216 в)
-216 в)
2) это я не совсем понимаю
3) (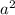 +2
+2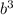 )*(
)*(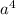 -2
-2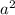
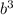 +4
+4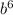 )=(
)=(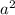 )в кубе+(2
)в кубе+(2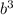 )в кубе=
)в кубе=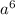 +8
+8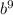 г)
г)
4) 3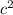 -48=3(
-48=3(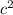 -16)=3(c-4)(c+4) б)
-16)=3(c-4)(c+4) б)
5) 7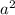 -42a+63=7(
-42a+63=7(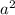 -6a+9)=7(a-3)в квадрате б)
-6a+9)=7(a-3)в квадрате б)
6) 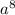 -
-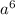 =
=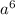 (
(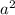 -1)=
-1)=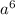 (a-1)(a+1) б)
(a-1)(a+1) б)
7) 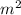 -
-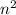 +m+n=(m-n)(m+n)+m+n=(m+n)(m-n+1) а)
+m+n=(m-n)(m+n)+m+n=(m+n)(m-n+1) а)
8) 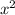 -
-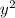 +14y-49=
+14y-49=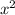 -(
-(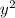 -14y+49)=
-14y+49)=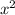 -(y-7)в квадрате=(x-(y-7))(x+(y-7))=(x-y+7)(x+y-7) в)
-(y-7)в квадрате=(x-(y-7))(x+(y-7))=(x-y+7)(x+y-7) в)
9) 81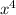 -1=(9
-1=(9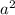 -1)(9
-1)(9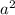 +1)=(3a-1)(3a+1)(9
+1)=(3a-1)(3a+1)(9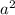 +1) а)
+1) а)
10) 49x-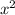 =0
=0
x(49-x)=0
x=0 49-x=0
x=49
в)
11) 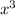 +3
+3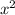 -x-3=0
-x-3=0
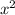 (x+3)-(x+3)=0
(x+3)-(x+3)=0
(x+3)(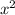 -1)=0
-1)=0
x+3=0 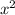 -1=0
-1=0
x=-3 x=-1 або x=1
г)
12) насчёт этого не уверена
(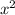 -2)в квадрате-4(
-2)в квадрате-4(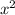 -2)+4=(
-2)+4=(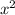 -2-2)в квадрате=(
-2-2)в квадрате=(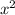 -4)в квадрате=((x-2)*(x+2))в квадрате
-4)в квадрате=((x-2)*(x+2))в квадрате
Все таки не удержусь и для начала покажу красивый без метода мат индукции, а потом уже с методом мат. индукции.
Первый .(собственно то, как, возможно, была выведена эта формула)
Обозначим сумму ряда за S:
1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+n(n+1)!/2^n = S
Рассмотрим также вс сумму S1:
2!/2 +3!/2^2 + 4!/2^3 +...+(n+1)!/2^n = S1
Тогда не трудно убедится, что
S+2S1 = 3*2!/2 + 4*3!/2^2 + 5*4!/2^3+...+(n+2)(n+1)!/2^n =
= 3!/2 + 4!/2^2+ 5!/2^3+...+(n+2)!/2^n = 2*( 3!/2^2 + 4!/2^3 +...+(n+2)!/2^(n+1) =
= 2(S1 -2!/2 + (n+2)!/2^(n+1))
То есть получаем равенство:
S+2S1 = 2S1 -2! + (n+2)!/2^n
Замечаем, что 2S1 сокращается:
S = (n+2)!/2^n - 2
Что и требовалось доказать.
Второй (метод математической индукции)
Проверим, что тождество верно для n = 1:
1*2!/2 = 3!/2 - 2
1 = 3 - 2 - верно.
Предположим, что утверждение справедливо для n = t, то есть:
1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+t(t+1)!/2^t = (t+2)!/2^t - 2
Докажем его справедливость для n = t+1
То есть нужно доказать, что:
1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+t(t+1)!/2^t + (t+1)(t+2)!/2^(t+1) = (t+3)!/2^(t+1) - 2
Нетрудно заметить, что:
1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+t(t+1)!/2^t + (t+1)(t+2)!/2^(t+1) =
= (1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+t(t+1)!/2^t) + (t+1)(t+2)!/2^(t+1) =
= (t+2)!/2^t - 2 + (t+1)(t+2)!/2^(t+1) = 2(t+2)!/2^(t+1) + (t+1)(t+2)!/2^(t+1) - 2 =
= (2+t+1)*(t+2)!/2^(t+1) - 2 = (t+3)((t+2)!/2^(t+1) - 2 = (t+3)!/2^(t+1) - 2
А значит, по принципу математической индукции, данное тождество доказано.