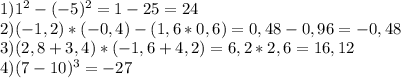Складіть числовий вираз і знайдіть його значення: 1)різниця квадратів чисел −1 і – 5

2)різниця добутків чисел −1,2 і −0,4 та чисел 1,6 і 0,6

3)добуток суми чисел 2,8 і −3,4 та суми чисел −1,6 і 4,2

4)куб різниці чисел 7 і 10

Question

Алгебра: Складіть числовий вираз і знайдіть його значення: 1)різниця квадратів чисел −1 і – 5 2)різниця добутків чисел −1,2 і −0,4 та чисел 1,6 і 0,6 3)добуток суми чисел 2,8 і −3,4 та суми чисел −1,6 і 4,2 4)куб різниці чисел 7 і 10

igoralekseev2 · Accepted Answer

Первый

Число единиц делится на три. Это могут быть только числа 3 (тогда число десятков равно2), 6 (тогда число десятков равно 4) или 9 (тогда число десятков равно 6).

Из трех чисел (23, 46 и 69) условию удовлетворяет лишь 46: 64 - 46 = 18.

ответ 46.

Второй

Можно и с уравнения: если число единиц обозначить за х, то число десятков будет 2/3х, и первоначальное число равно 10*2/3х + х = 23/3х

А число с переставленными цифрами запишется в виде 10х + 2/3х = 32/3х

Их разность равна по условию 18. Составляем уравнение32/3х - 23/3х = 18, откуда

х = 18/3 = 6. Тогда число десятков исходного числа будет равно 6*2/3 = 4.

ответ: 46

MOGZ ответил