1) Если в какой-то части уравнения находится выражение в скобках. Чтобы раскрыть скобки, посмотрите на знак перед скобками. Если стоит знак плюс, при раскрывании скобок в записи выражения ничего не поменяется: просто уберите скобки. Если стоит знак минус, при раскрытии скобок необходимо поменять все знаки в выражении, стоящем изначально в скобках, на противоположные. Например, -(2х-3)=-2х+3.
2) Перемножение двух скобок.
Если в уравнении присутствует произведение двух скобок, раскрытие скобок происходит по стандартному правилу. Каждый член первой скобки перемножается с каждым членом второй скобки. Полученные числа суммируются. При этом произведение двух "плюсов" или двух "минусов" дает слагаемому знак "плюс", а если множители имеют разные знаки, то слагаемое получает знак "минус".
Рассмотрим пример.
(5х+1)(3х-4)=5х*3х-5х*4+1*3х-1*4=15х^2-20х+3х-4=15х^2-17х-4. 3Раскрытием скобок иногда также называют возведение выражения в степень. Формулы возведения в квадрат и в куб надо знать наизусть и помнить.
(a+b)^2=a^2+2ab+b^2
(a-b)^2=a^2-2ab+b^2
(a+b)^3=a^3+3a^2*b+3ab^2+b^3
(a-b)^3=a^3-3a^2*b+3ab^2-b^3
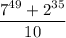будет сократимой, если 
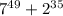делится на 
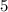или 
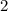. А для того чтобы число делилось на 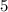, нужно чтобы это число заканчивалось на 
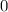или на 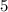. А для делимости числа на 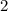нужно чтобы число заканчивалось на четную цифру.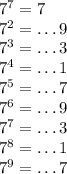
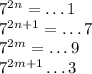
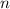— чётное натуральное число, 
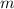— нечётное натуральное число.
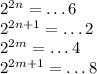
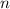— чётное натуральное число, 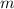— нечётное натуральное число.
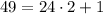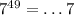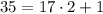, то 
.
, то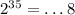 
.
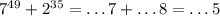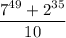. делятся на 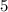, значит, дробь сократима.
