Пусть  - количество дней, за которое работу может выполнить первая бригада. У второй это займёт на 8 дней больше, то есть,
- количество дней, за которое работу может выполнить первая бригада. У второй это займёт на 8 дней больше, то есть, 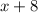 . Работая вместе, они выполнили её за 3 дня. Составляем уравнение:
. Работая вместе, они выполнили её за 3 дня. Составляем уравнение:
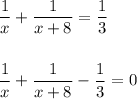
Приводим дроби к общему знаменателю 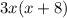 :
:
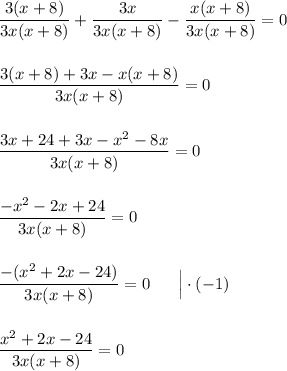
Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. То есть:
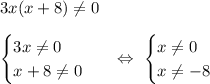
Приравниваем числитель к нулю:
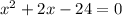
По теореме Виета:
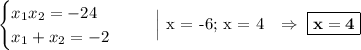
-6 не подходит, поскольку количество дней не может быть отрицательным числом. Поэтому получаем, что первая бригада может выполнить работу за 4 дня.
ответ: за 4 дня.
1) значение функции, если значение аргумента равно -2;
2) значение аргумента, при котором значение функции равно 13;
3) проходит ли график функции через точку А(-1; -7).
2. Постройте график функции y = 2x+ 1. Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно 1;
2) значение аргумента, при котором значение функции равно -3.
3. Не выполняя построения, найдите координаты точек пересечения графика функции
y = -2x+ 6 с осями координат.
4. При каком значении k график функции y = kx + 4 проходит через точку А(-3; -17)?
Как то так если не очень значит спиши с интернета
1) 15 км/ час.
2) 15 часов.
3) 13.
4) 12.
Объяснение:
1. Решение.
Пусть х км/час - собственная скорость катера
Скорость по течению равна х+3 км/час
Время на движение по течению затрачено
t1=S1/v1 = 5/(x+3) часов.
Время на движение по озеру затрачено
t2=S2/v2 = 8/х часов.
Общее время t1+t2=1 час.
Составим уравнение:
5/(x+3) + 8/x = 1;
5x + 8(x+3)=x(x+3);
5x+8x+24 = x²+3x;
x² - 10x -24 = 0;
По теореме Виета
х1 = 12; х2 = -2 - не соответствует условию
х=12 км/час - собственная скорость катера.
х+3=12+3=15 км/час - скорость катера по течению.
***
2) Решение.
Производительность двух труб равна 1/10 часть /час.
Пусть первая труба наполняет бассейн за х часов. Тогда ее производительность равна 1/х часть/час
Вторая труба наполняет на 15 часов дольше: х+15 часов и
ее производительность равна 1/(х+15) часть/час.
Составим уравнение:
1/х + 1/(х+15)=1/10;
10(х+15) + 10х = х(х+15);
10х + 150 +10х = х²+15х;
х²+15х -10х -10х -150=0;
х²-5х -150=0;
х1=15; х2=-10 - не соответствует условию.
х=15 часов - время заполнения первой трубой.
***
3) Решение.
Обозначим гипотенузу через х. Тогда один из катетов равен х-1, а второй х-8.
По теореме Пифагора
х² = (х-1)² + (х-8)²;
х²=х²-2х+1 + х²-16х+64;
х²-18х+65=0;
x1=13; x2=5;
Если гипотенуза равна 13, то катеты равны 13-1=12 и 13-8=5.
Если гипотенуза равна 5, то катеты равны 5-1 = 4 и 5-8=-3 - не соответствует условию.
Следовательно гипотенуза равна 13.
***
Решение.
Пусть меньшая сторона равна х. Тогда большая равна х+3.
По теореме Пифагора
x²+(x+3)² = 15²;
x²+x²+6x+9=225;
2x² +6x - 216=0;
x²+3x - 108=0;
x1=9; x2= - 12 - не соответствует условию.
х=9 меньшая сторона.
х+3=9+3=12 = большая сторона прямоугольника