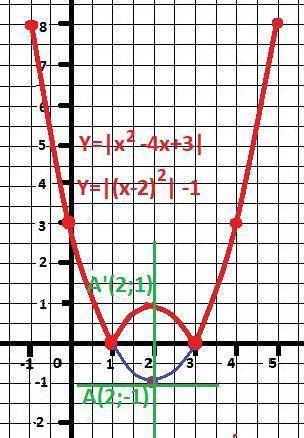
ДАНО: f(x) = x² - 4x + 3.
Пошаговое объяснение:
Это парабола с ветвями вверх. Для того чтобы найти её вершину преобразуем уравнение к полному квадрату.
x² - 4*x + 3 = (x² -2*x*2 + 2²) - 4 + 3 = (x - 2)² - 1.
Прибавили и отняли 2² = 4.
Получаем координаты вершины параболы - точки А(2;-1).
Но отрицательную часть графика надо отразить относительно оси ОХ - в точку A'(2;1).
Парабола четная и симметричная. Построение по точкам - относительно прямой Х = 2.
x = y = 1
x = 1, 3, y = 0
x = 0, 4, y = 3
x = -1, 5, y = 8
Общий вид комплексного числа следующее z=r(cos phi+isin phi). Для этого сначала найдем модуль комплексного числа
|z|=sqrt{(-1)^2+1^2}=sqrt{2}
z=-1+i=|z|(-frac{1}{|z|}+frac{1}{|z|}i)=sqrt{2}(-frac{1}{sqrt{2}}+frac{1}{sqrt{2}}i)
cos phi=-frac{1}{sqrt{2}}\ sinphi=frac{1}{sqrt{2}}
Косинус отрицателен, а синус положителен, значит это вторая четверть и угол нужно найти именно во второй четверти, это будет phi=frac{3pi}{4}
z=-1+i=sqrt{2}(-frac{1}{sqrt{2}}+frac{1}{sqrt{2}}i)=sqrt{2}(cosfrac{3pi}{4}+isinfrac{3pi}{4})=sqrt{2}e^{ifrac{3pi}{4}}