Каким бы мы не решали, стоит разложить выражение на множители.
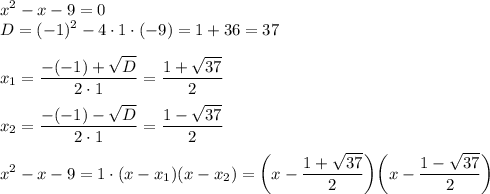
Тогда имеем: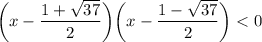 
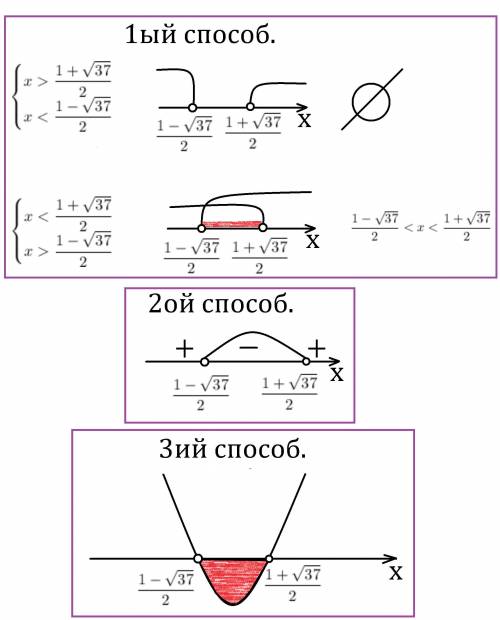
1ый через знак множителей):
Произведение будет отрицательным, если один из множителей отрицательный, а другой положительный.
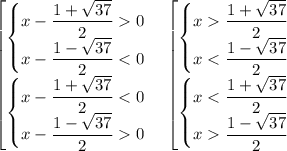
ответ: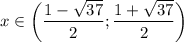 
2ой метод интервалов):
Отмечаем на координатной прямой точки, в которых выражение обращается в ноль. И выкалываем их т.к. неравенство строгое (<, а не ≤). Мы получили 3 интервала. Перед множителями знак положителен, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (нету чётных степеней, где знак может не измениться). Нас интересует, когда меньше, поэтому выбираем интервалы с минусом.
ответ: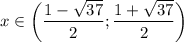
3ий графический):
y = x²-x-9
Это парабола, ветви которой направлены вверх. У функции есть два нуля:
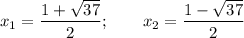. Нас интересует, когда меньше нуля, это когда график ниже оси Ox.
ответ: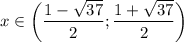
Вопросы в личные сообщения.